记录刷题日志

2.19

Z变化利用一个字符串数组存储,简单模拟即可
整数的反转看似简单但是并非如此,注意到反转的基本操作: res = res * 10 + x % 10 ,并且需要每一次都检测 res < INT_MIN || res > INT_MAX是否为 false , 推导过程可以参考官方的题解(注意力惊人!!!)
正则匹配恭喜成功入选 Hard , 有意思的一道题目,感觉和编辑距离问题类似

2.20

字符串转换整数(atoi) 模拟题目,没什么意思
最接近的三数之和排序 + 三指针,和三数之和一模一样,甚至更简单
两数相除算是思路惊奇的一道题目,类似于不断二分,核心代码如下:

long div(long a , long b) {
	if(a < b) return 0;
	long tb = b;
	long count = 1;
	while((tb + tb) <= a) {
		count = count + count;
		tb = tb + tb;_	
	}
	return count + div(a - tb , b);
}

注意到最后一句话等效于: $$ k + \frac{a - kb}{b} = \frac{a}{b} $$

2.21

有效的数独简单模拟 + 哈希 , 没有什么好说的
外观数列简单,没有什么好说的
串联字符串所有单词的子串入选 Hard

2.22

字符串相乘比较有意思的一个题目,本质上就是对于竖式的一个优化,只需要维护一个数组,并且把结构的每一个位存储在数组中即可,但是注意到一个结论, num1[i] 和 num2[j] 相乘的结构总共有两位,一个在 res[i + j] 的位置上面(这里就是进位) , 另外一个在 res[i + j + 1] 上面,可以这样理解(比如对于num2 , 索引的位置也就是表示开始的位置,对于 num1 只是加上了一个偏移即可):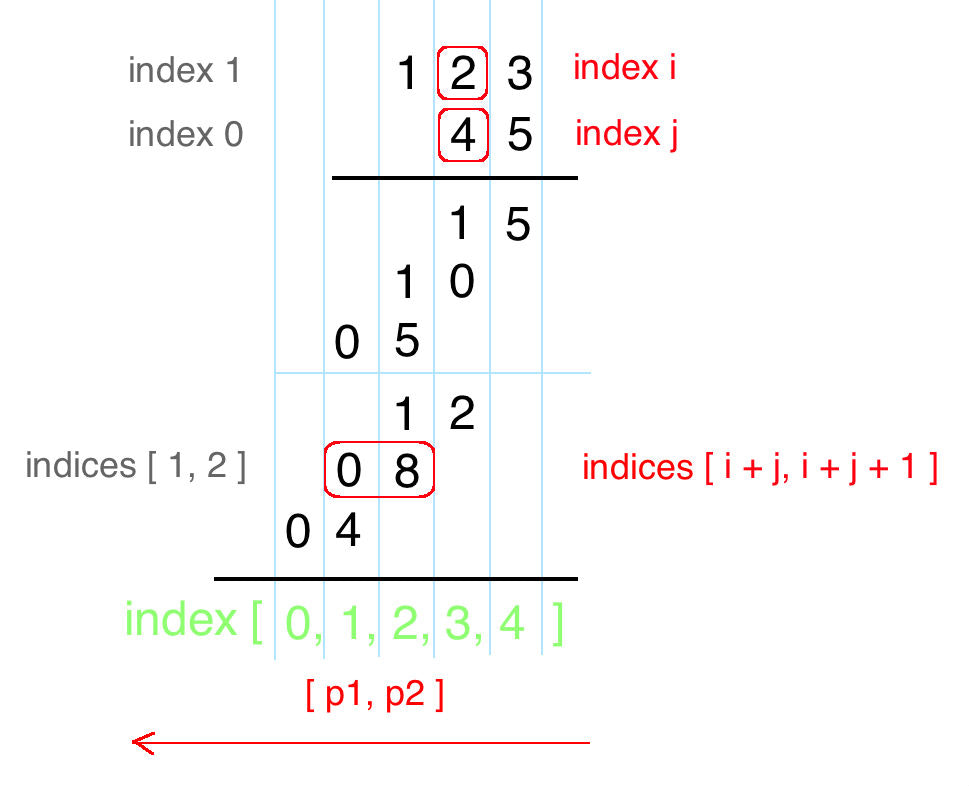
Power(x,n) 快速幂,可以使用二进制的方法理解或者使用分治法来理解 $$ n = 2^0 b_1 + 2 ^ 1 b_2 + 2^2 b_3 + ... + 2^nb_{n + 1} $$ $$ x^n = x^{2^0 b_1 + 2 ^ 1 b_2 + 2^2 b_3 + ... + 2^nb_{n + 1}}= x^{2^0b_1}x^{2^1b_2}x^{2^2b_3}...x^{2^nb_{n + 1}} $$ 所以每一次只需要不断取得 n 的二进制位置并且把 x 平方即可,核心代码如下:

while(n != 0) {
	if((n & 1) == 1) res *= x;
	x *= x;
	n >>= 1;	
}

当然也可以使用分治的方法: Pasted image 20250222154755.png

3 . 通配符匹配和正则表达式类似,但是更加简单,使用 dp 即可,但是注意到通佩符('*')在最后并且匹配 0 个字符的情况即可

2.23

写了一天的 CURD , 没有刷题 ...

2.24

插入区间个人感觉自己的写法corner case太多了,也就是分区间和最后一个区间交叉,和区间在最后一个区间前面两种情况,利用一个变量记录是否插入即可
旋转链表倒数第 K 个节点 + 链表操作,比旋转数组还简单
排列序列我的做法是和HOT100 中最后一个排列有关的,代码随想录里面真是写的依托 , 还让找规律,不抓住事物的本质,官方题解中的答案感觉比较困难,也就是无法每一次找到哪一个元素为排列的第一个元素,可以看一下官方题解中的题目,技巧太多了,之后可以看一下吧

2.25

合并有序数组利用三个指针,三个指针分别为 i = m - 1 , j = n - 1 k = m + n - 1 , 也就是 k 指向了新数组的最后一个位置
反转链表 II 注意使用虚拟头节点,避免对于是否头节点的讨论即可

2.26

实验报告,课太多了...

2.27

开始刷面试经典 150 题目了,大部分原题,刷了 11 道题目

删除数组中的重复项II 我的方法是利用一个 curCount 来记录出现的次数,题解中的方法是利用 nums[r] != nums[l - x] 来进行求解,其实都差不多,最终返回 l
H指数我的方法是利用哈希表进行统计,从后面向前面统计,每一次累积加上 hash[i] , 直到cnt >= i 就可以返回 i 了,类似于灵神的方法,但是注意到大于 n 的可以作为 n 计算,所以空间就是 n + 1 就可以了,但是当n 比较大的时候还是我的方法比较好

xzw'blog