机器学习

机器学习中的基本概念

特征: 表示需要预测对象的特点(比如芒果的大小,形状颜色等特征信息)
标签: 表示最终需要预测的变量(比如芒果的甜度等信息),可以是离散的也可以是连续的
一个标记好特征以及标签的对象可以看成一个样本
一组样本构成的集合称为数据集（Data Set）．一般将数据集分为两部分：数据集也训练集和测试集．训练集（Training Set）中的样本是用来训练模型的，也叫训练样本（Training Sample），而测试集（Test Set）中的样本是用来检验模型好坏的，也叫测试样本（Test Sample）
可以使用一个D维的向量来表示样本的特征,叫做特征向量: $$ {\mathbf x} = [x_1 , x_2 , ...,x_D]^T $$
训练集由N个样本组成,每一个样本都是独立同分布的,记为: $$ {\mathcal D} = {({\mathbf x}^{(1)} , {\mathbf y}^{(1)}) , ({\mathbf x}^{(2)} , {\mathbf y}^{(2)}) , ... , ({\mathbf x}^{(N)} , {\mathbf y}^{(N)})} $$
给定训练集需要从函数集合 $$ \mathcal F = {f_1(\mathbf x) , f_2(\mathbf x) ... } $$ 中找到一个最有的函数f(x)来近似表示特征向量与标签之前的关系,也就是: $$ \widehat y = f^(\mathbf x) $$ 或者条件概率 $$ \widehat p(y|\mathbf x) = f_y^(\mathbf x) $$
寻找着一个最优函数的过程叫做学习,一般通过学习算法来完成
一般可以通过测试集确定模型的准确率:
机器学习的基本流程:

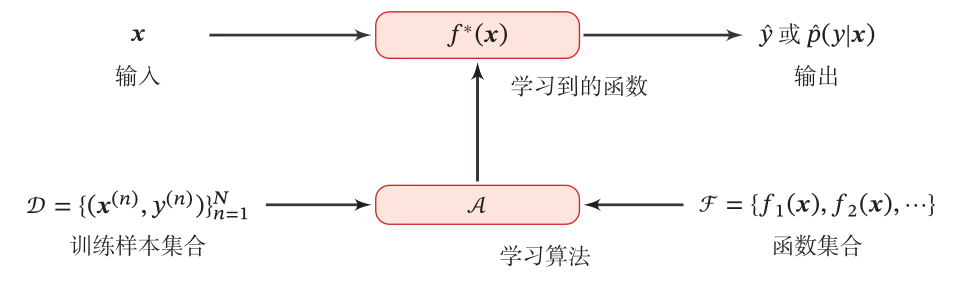
机器学习的三要素

模型

也就是上面说的最优函数,一般可以从一个函数集合(这里成为假设空间中找到这一个最优模型): $$ {\mathcal F} = {f({\mathbf x};\theta)|\theta \in \mathbb R^D} $$
线性模型: $$ f(\mathbf x ; \theta) = {\mathbf \omega}^T{\mathbf x} + b $$
非线性模型:

学习准则

一般可以通过期望风险来衡量,定义为: $$ \mathcal R(\theta) = \mathbb E_{(x,y) - p_r(x,y)}[\mathcal L(y,f(\mathbf x;\theta))] $$
其中也就是测试集中每一个点的风险函数的取值的均值

损失函数

用于衡量模型预测与真实标签之间的差异
常用的损失函数:
01损失函数: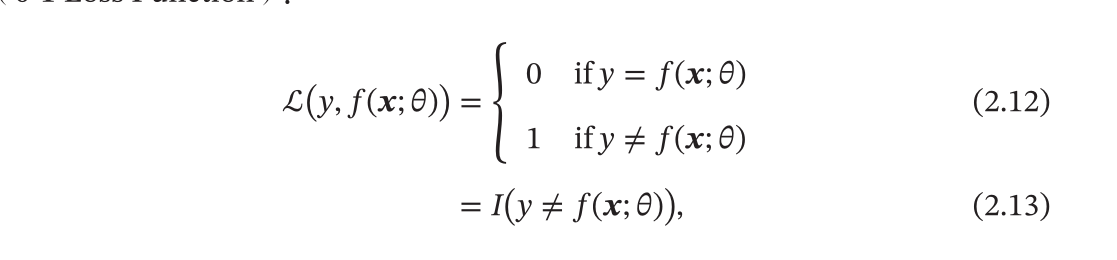
平方损失函数:
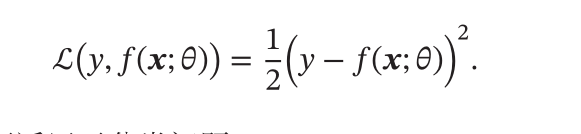
交叉熵损失函数(一般用于分类问题),类似于期望

风险最小化

一般利用经验风险评估模型的准确性:
同时为了防止过拟合,一般可以引入参数的正则化来限制模型的能力,这一种准册叫做结构风险最小化:
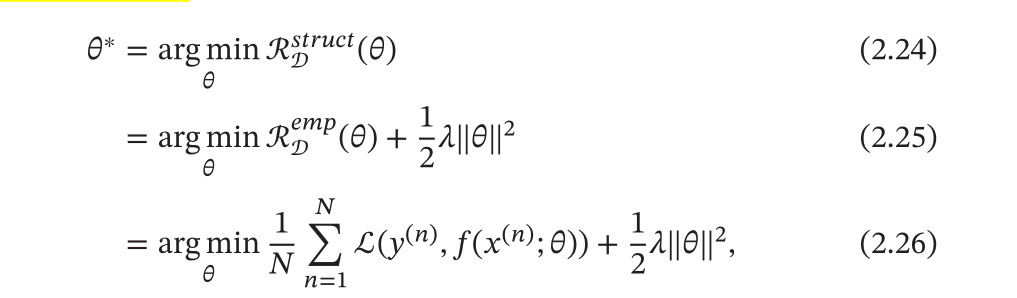
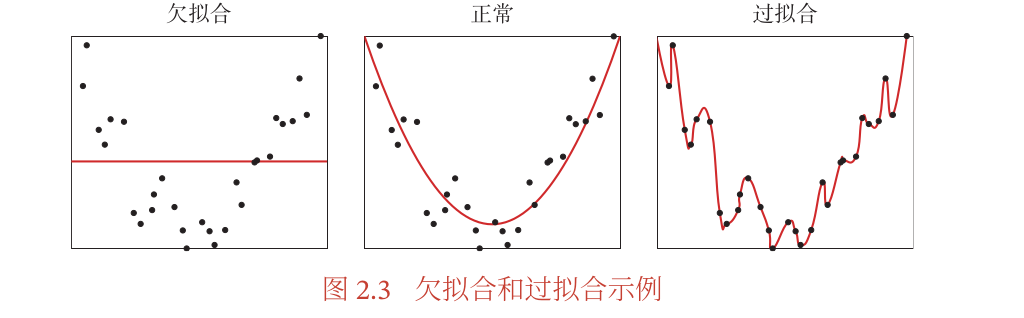
欠拟合,过拟合和正常的情况:

优化算法

可以看成利用寻找最优模型的算法,是一种迭代算法(寻找经验风险or结构风险最小的点)

梯度下降法

利用如下公式进行参数的迭代:

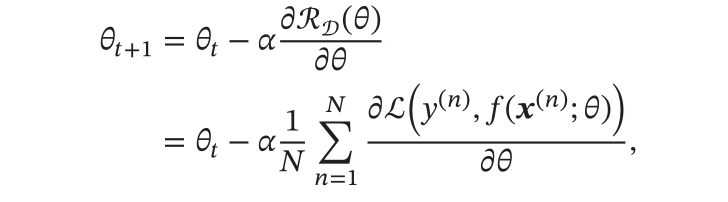
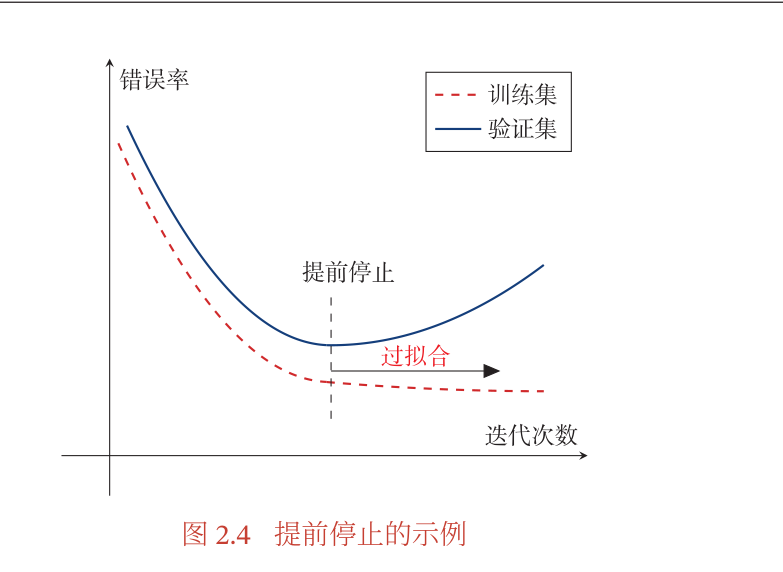
提前停止

划分出验证集,每一次将得到的模型在验证集上面进行验证,如果发现验证集中的错误率不再下降就会停止,可以防止过拟合

随机梯度下降

为了防止每一次迭代都需要计算训练集中每一个样本的偏导数,所以可以参用随机梯度下降法,也就是随机选择一个样本进行梯度下降:

批量梯度下降

也似乎为了减少梯度下降的复杂度,每一次只是抽取一个小部分的元素

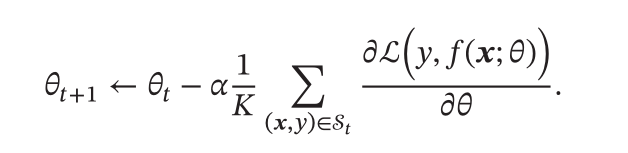
机器学习算法的种类

监督学习(回归,分类,结构化等问题)
无监督学习
强化学习
三者的差别:
交叉验证:

线性模型

Logistic回归

首先回归问除了需要获取一个判别函数($f(x; \mathbf \omega) = {\mathbf \omega}^T {\mathbf x} + b$ ) 之外还需要确定一个决策函数$g(x)$ 用于把判别函数的结果映射到一个有效的类别上
Logistic回归可以利用于解决二分类的问题,考虑后验概率: $$ p(y = 1 | {\mathbf x}) = g(f({\mathbf x}; {\mathbf \omega})) $$
Logisitc回归中使用Logistic函数作为激活函数,比如标签$y = 1$ 的后验概率为 $$ p(y = 1 | x) = \sigma({\mathbf \omega}^{T}{\mathbf x}) = \frac{1}{1 + \exp(-{\mathbf \omega}^{T}{\mathbf x})} $$
这里的$\omega$ 增广权重矩阵 , $\mathbf x$ 是增广特征矩阵
从而可以得到: $$ p(y = 0 | {\mathbf x}) = 1 - p(y = 1 | {\mathbf x}) $$
结合上面两个式子可以得到: $$ {\mathbf \omega}^{T}{\mathbf x} = log{\frac{p(y = 1 | {\mathbf x})}{p(y = 0 | {\mathbf x})}} $$
参数学习的过程中使用交叉熵函数作为损失函数并且利用梯队下降算法来优化参数
后验概率为: $$ \widehat y^{(n)} = \sigma({\mathbf \omega}^{T}{\mathbf x}^{{n}})
$$
所以可以得到: $$ p_r(y^{n} = 1 | {\mathbf x}^{n}) = y^{(n)}
$$ $$ p_r(y^{n} = 0 | {\mathbf x}^{n}) = 1- y^{(n)} $$

Softmax回归

Softmax中预测最终结果属于类别c的条件概率为,其中x为样本: $$ p(y = c | \mathbf x) = softmax({\mathbf \omega}c^T{\mathbf x}) = \frac{exp(\mathbf \omega_c^T{\mathbf x})}{\sum\limits {c' = 1}^{C} exp({\mathbf \omega}_{c'}^T{\mathbf x})} $$
决策函数使用如下函数:
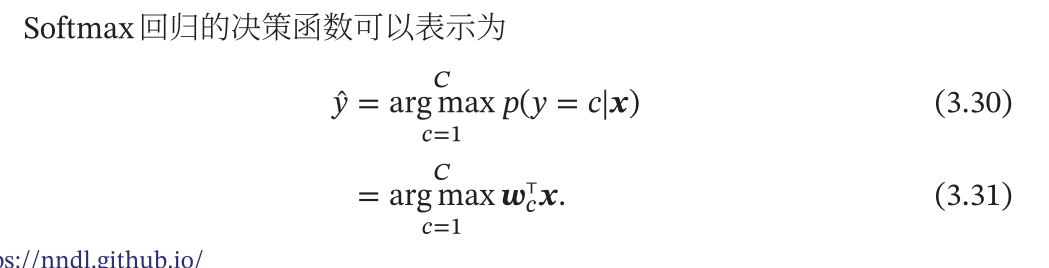
但种类为2的时候就会退化成Logistic回归
利用向量形式可以表示为:

参数学习

这里使用交叉熵模型作为损失函数,那么可以得到风险函数如下:
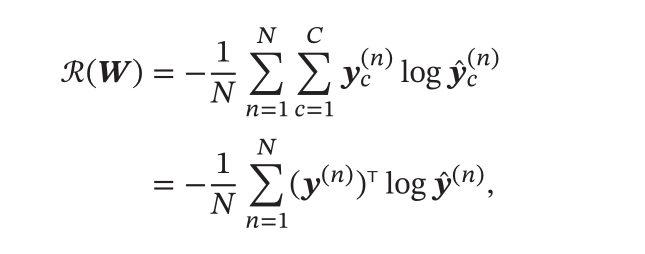
利用梯度下降算法求解参数,这里需要求解风险函数的梯度,求解过程如下:
从而利用梯度下降算法进行参数的迭代更新就可以求解得到最优的矩阵 $\mathbf W$

感知器

感知器是一种最简单的人工神经网络,只有一个神经元,对于外界的特征信息只会输出1或者-1 , 所以最终的分类准则为: $$ \widehat y = sgn({\mathbf \omega}^T{\mathbf x}) $$

参数学习

学习策略:
学习策略可以抽象为如下的代码:
参数学习的过程(注意注意这里使用了梯度下降算法,每一次需要利用向量的运算规则来决定新的向量需要指向哪一个位置):

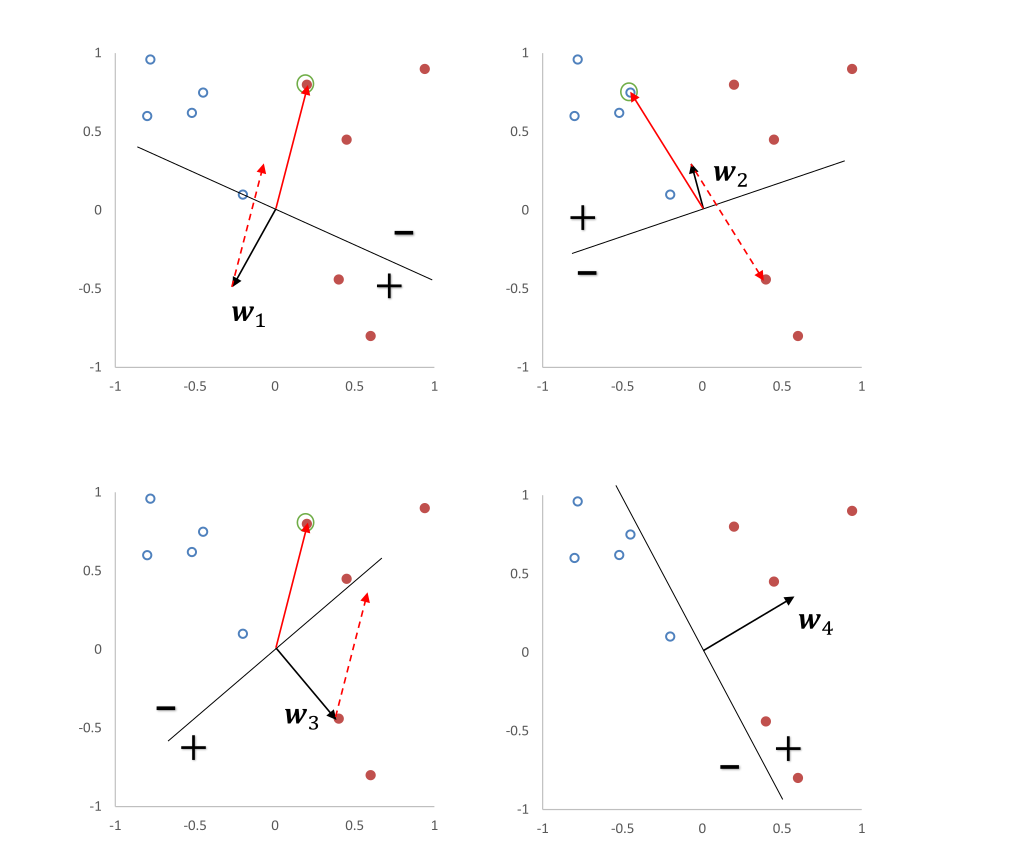
参数平均感知器

由于这一种利用错误数据决定变化方向的规则会使得后面的错误数据相对于前面的错误数据的影响更大,所以引出一种利用参数平均感知器也就是给每一个迭代的到的模型赋予一个权值,从而利用这一个权值得到最终的结果,同时又可以利用平均值
如果扩展到多分类,那么就需要建立一个广义的感知机模型:

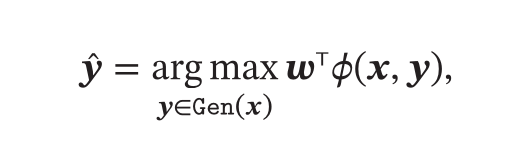
支持向量机

支持向量机也是一种二分类算法,也是为了寻找一个超平面对于样本进行分类,这里寻找的方法就是不断计算样本距离目前的模型的平面的距离,从而不断调整模型的参数(比如利用梯度下降算法等方式)(注意训练的过程是参数不断更新的过程,需要不断调整模型的参数)

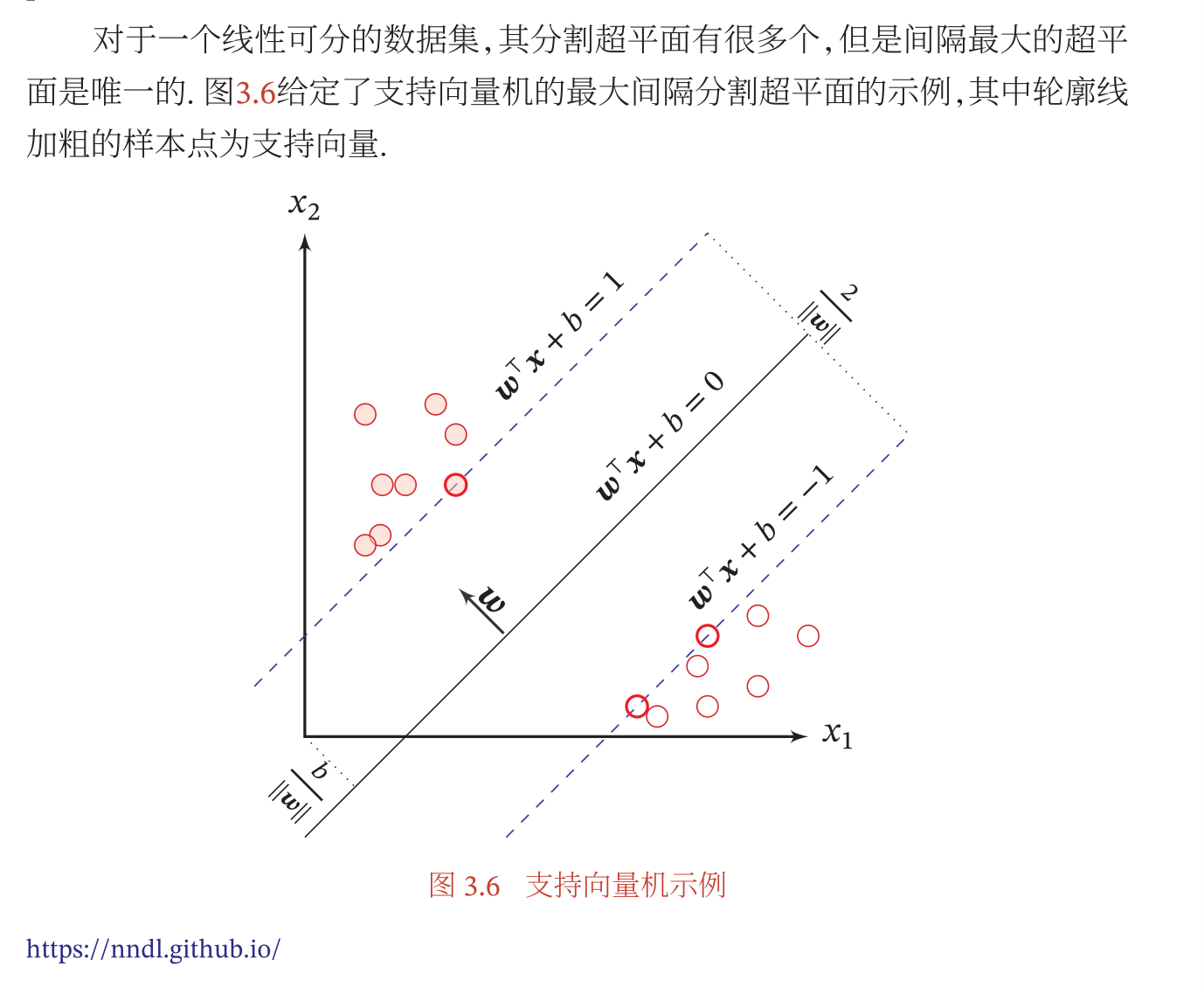
参数学习

一般利用拉格朗日法进行参数的学习(注意随着训练集的数据的不断读取,模型参数会不断调整)
利用拉格朗日对偶函数就可以求解最优的参数 $y^*$ 了,知道最优的参数之后可以使用支持向量的任意一个点求解偏置b

核函数和软间隔

核函数用于把原始空间映射到更加高维度的空间,这一个过程中需要使用核函数
软间隔: 类似于参数的正则化,放置样本在线性不可分开的区间里面无法找到最优解

损失函数对比

Logistic的损失函数利用了交叉熵损失函数
感知器损失函数
支持向量器损失函数
平方损失函数
效果对比(最终得到的模型的yf(x;w)大并且损失函数的值小就是比较好的模型):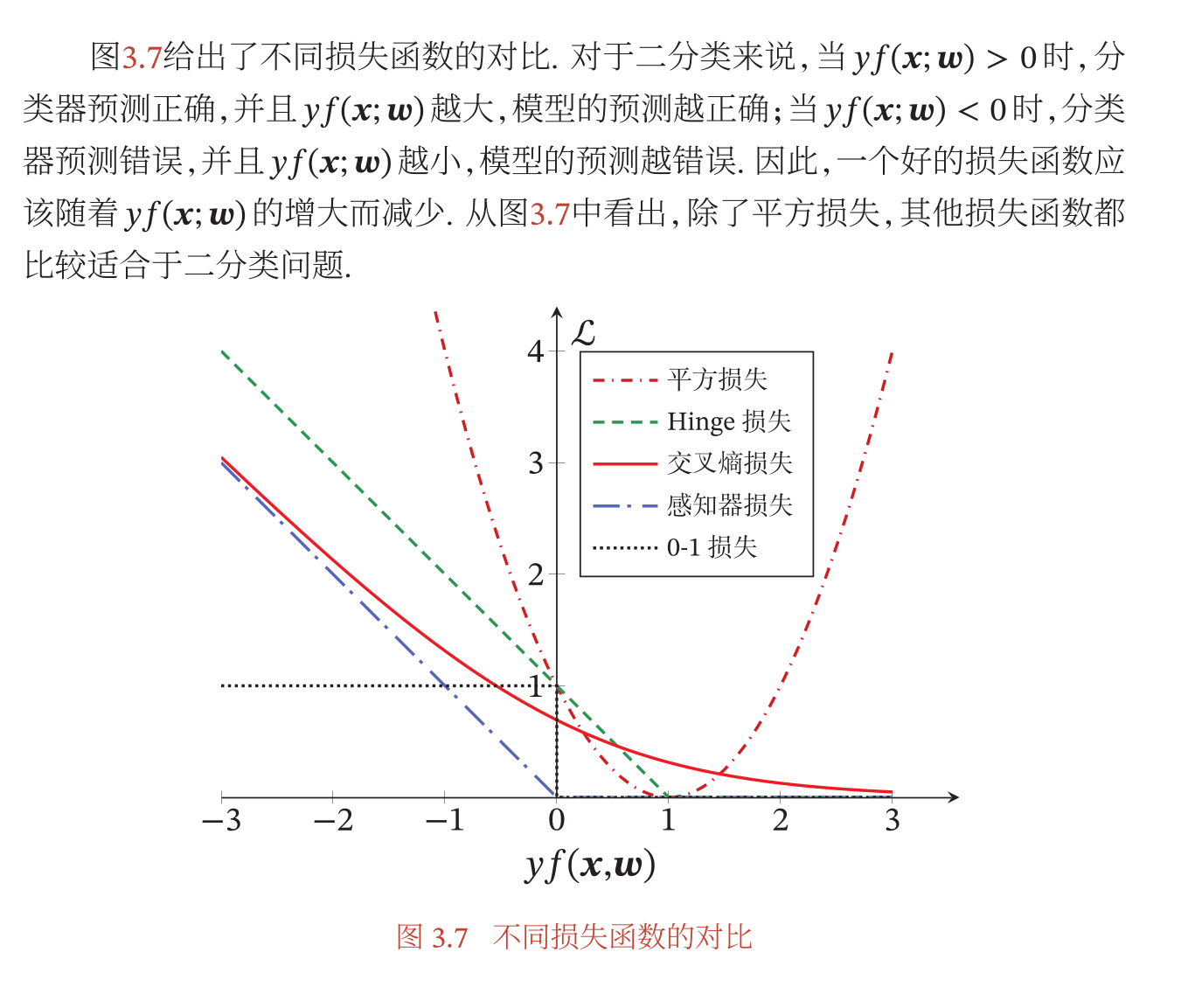
几种线性模型的对比:

基本模型

前馈神经网络

神经元

人工神经元是对于生物神经元的一种模拟,生物神经元通过树突接受信息,通过突触发送信息给之后的神经元,所以人工神经元也是一样的(接受信息,输入信号到达一定的阈值之后就会使得神经元处于激活状态,从而产生电脉冲完成信息的传递)

激活函数

假设一个神经元接受$D$个输入$x_1,x_2,x_3 ... , x_D$ ,可以利用向量 $\mathbf x = [x_1,x_2,x_3, ... , x_D]$ 来表示输入,并且使用净输入量来表示一个神经元获得的输入信息的加权和 $$ z = \sum_\limits{d = 1}^D{\omega}_d{x}_d + b = {\mathbf \omega}^T{\mathbf x} + b $$
z经过一个非线性函数f(.)之后就可以得到神经元的活性值a,其中 $a = f(z)$ ,非线性函数f(.) 就是激活函数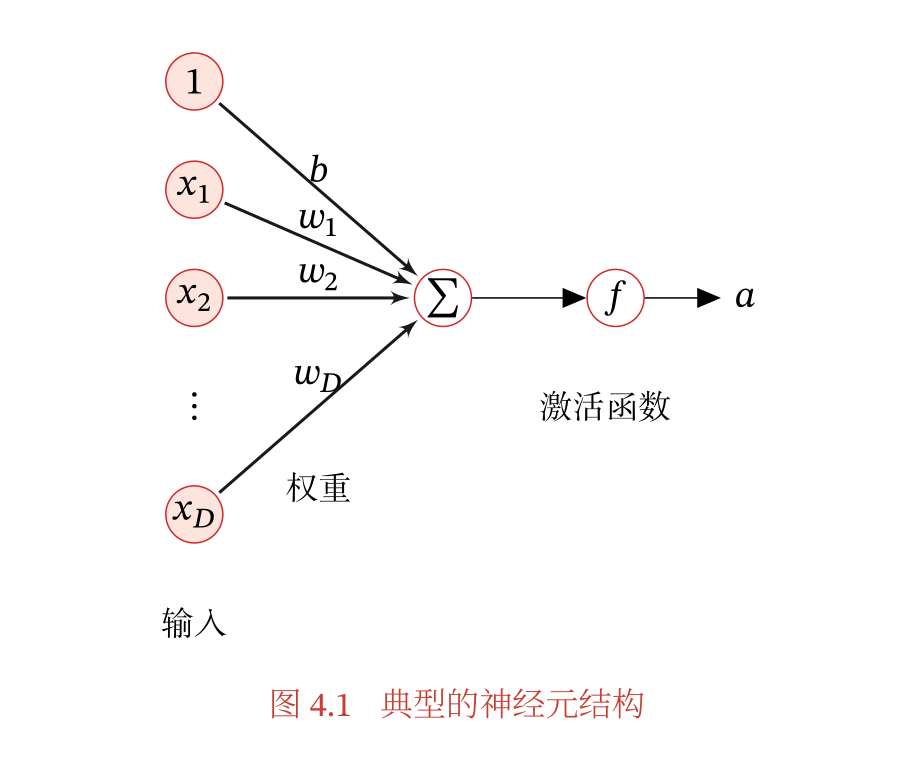

Sigmoid函数

一种S型曲线函数,两端饱和函数(也就是两个极限位置都是趋于一个常数)
Logistic函数,定义如下: $$ \sigma(x) = \frac{1}{1 + exp(-x)} $$
性质如下: $$ \sigma^{'}(x) = \sigma(x)(1 - \sigma(x)) $$
当信号比较小的时候,活性基本为0,信号比较大的时候活性接近与1
Tanh函数,定义如下: $$ tanh(x) = \frac{exp(x) - exp(-x)}{exp(x) + exp(-x)} $$
也就是: $$ tanh(x) = 2\sigma(2x) - 1 $$
Tanh函数的输出是零中心化的,Logistic函数的输出恒大于0,非零中心化的输出会使得后面一层的神经元的输入发生偏置从而使得梯度下降的收敛速度变慢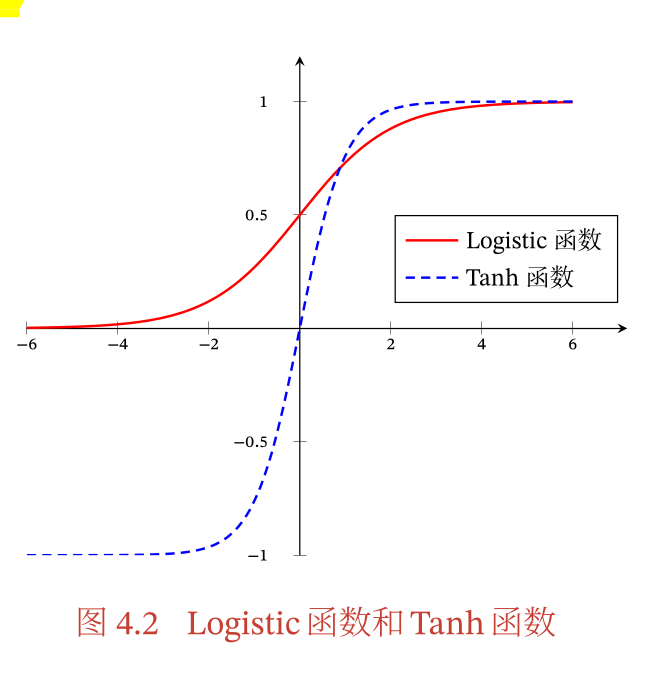
Hard Logistic函数和Hard Tanh函数,都是一种近似的线性分段函数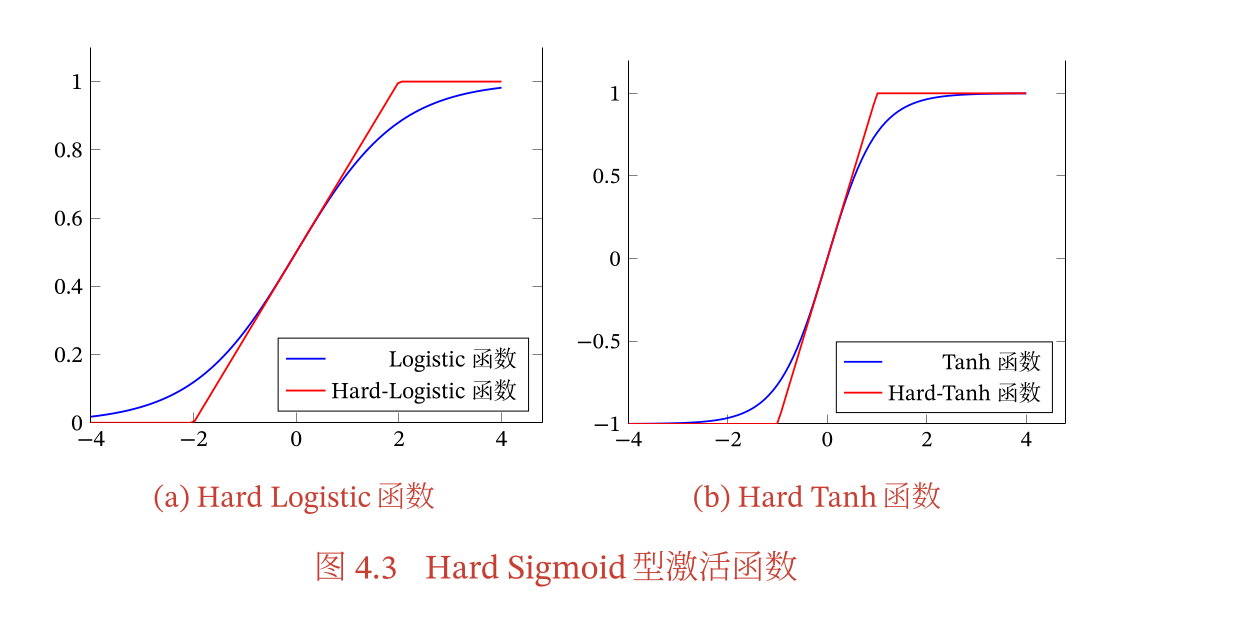

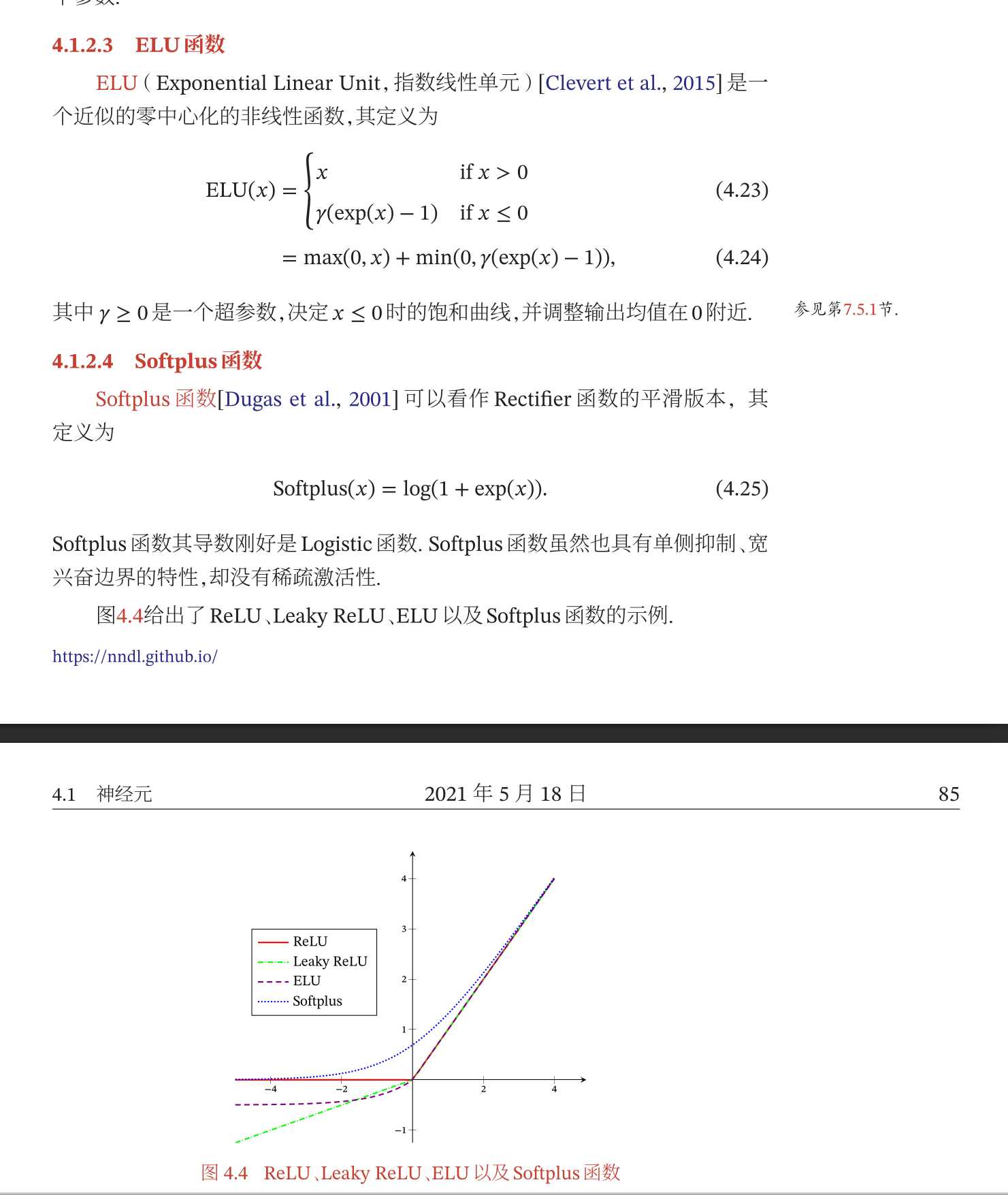
ReLU函数

一种斜坡函数,定义如下: $$ ReLU(x) = \begin{cases} x & \text{if } x >= 0 \ 0 & \text{if } x < 0 \end{cases} = max(0,x) $$
优点: 操作简单,稀疏性比较好(分布均匀),大于0时导数为1
缺点: 非零中心化,如果一个神经元接收到负信号就会死亡无法被激活
带泄漏的ReLU 和带参数的ReLU

ELU函数和Softplus函数

Pasted image 20241112171507.png

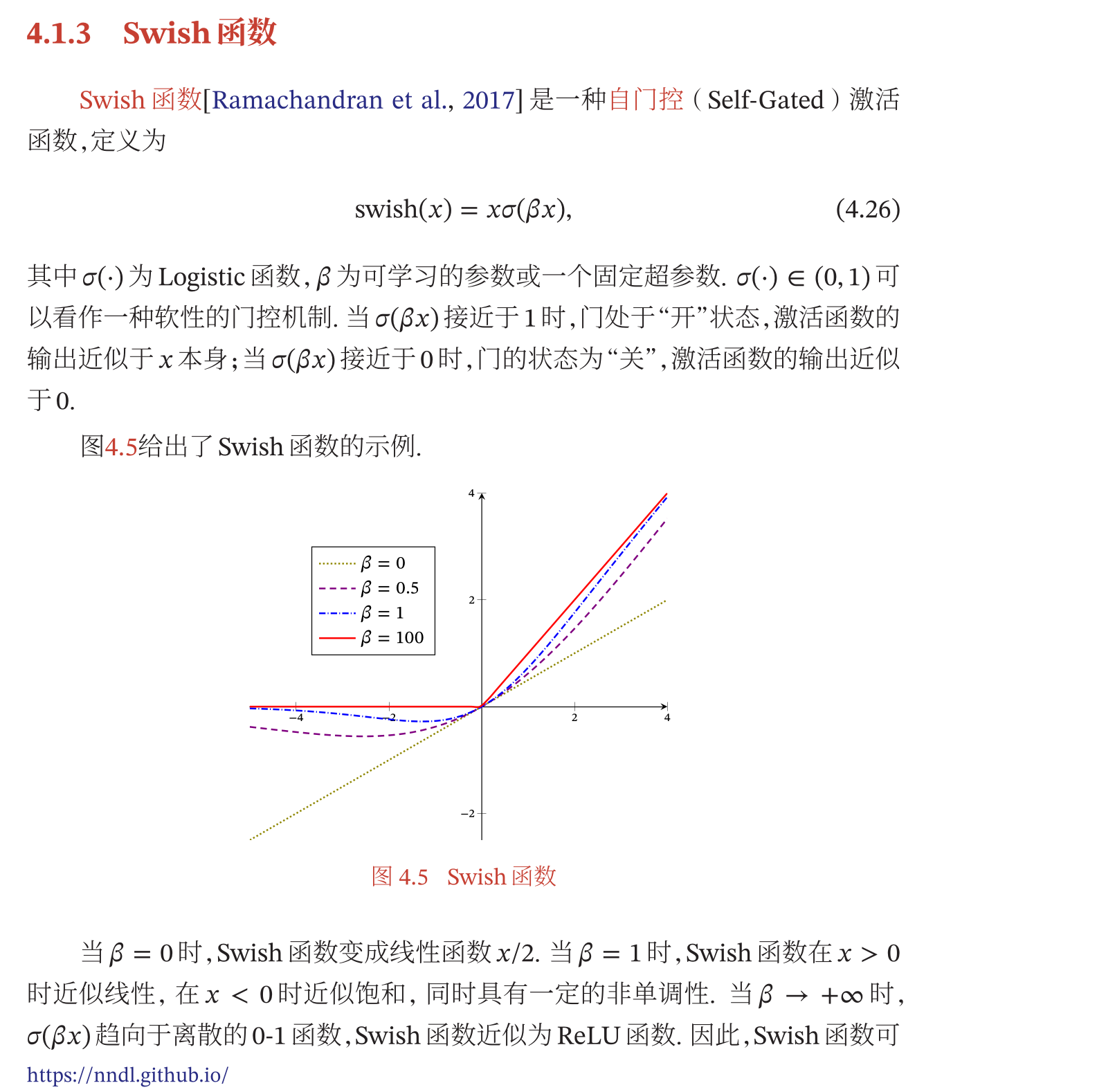
Swish函数

一种自门空控激活函数

Maxout单元

用于描述上一层神经元的整体输出,

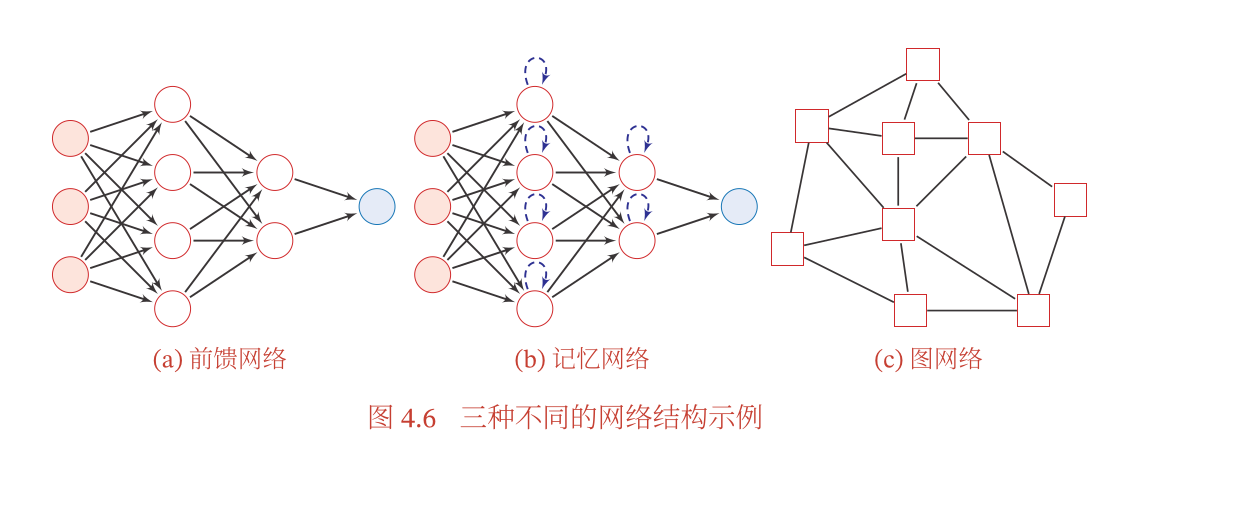
网络结构

前馈网络: 每一个神经元按照接受信号的先后顺序分为不同的组,每一层可以看成一个神经层,每一层的神经元接受前面一层的输出并且输出到下一层神经元,信息都是朝着一个方向传递的包含全连接前馈网络和卷积神经网络
记忆网络: 反馈网络,网络中的神经元不但可以接受其他神经元的信息还可以接受自己的历史信息,包含循环神经网络等
图网络: 应用与图结构的数据结构,同时也是前馈网络和记忆网络的优化,包含各种不同的实现方式,比如图卷积网络等

前馈神经网络

也叫做多层感知器,因为前馈神经网络其实是多层的Logistic回归模型
第 0 层称为输入层，最后一层称为输出层，其他中间层称为隐藏层．整个网络中无反馈，信号从输入层向输出层单向传播，可用一个有向无环图表示．
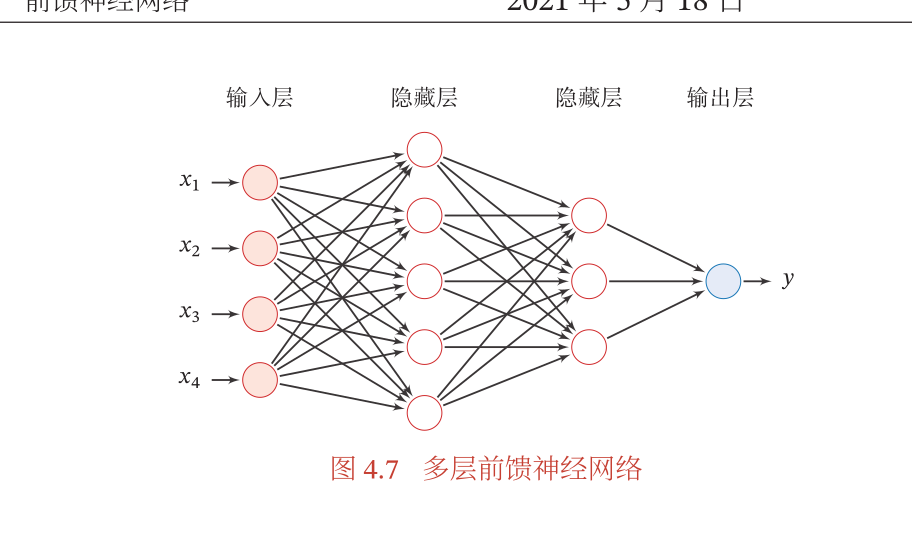
相关参数如下:
前馈神经网络利用如下迭代进行信息传递: $$ {\mathbf z}^{(l)} = {\mathbf W}^{(l)}{\mathbf a}^{(l - 1)} + {\mathbf b}^{(l)} $$ $$ {\mathbf a}^{(l)} = f_l({\mathbf z}^{(l)}) $$
每一层可以看成一个仿射变化(也就是从一个空间映射到另外一个空间的变化),整个网络可以看成一个复合函数 $\phi({\mathbf x};{\mathbf W},{\mathbf b})$ , 所以通过不断的传递,最后就可以得到第L层的输出作为整个函数的输出: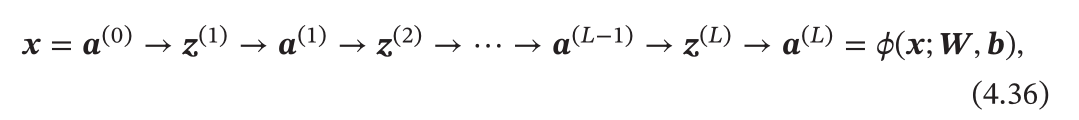 其中 𝑾, 𝒃 表示网络中所有层的连接权重和偏置
根据通用近似定理,前馈神经网络可以用于拟合各种连续非线性函数

应用到机器学习

比如用于分类问题: 注意神经网络的作用可以看成进行函数的一个仿射变化,也就是可以对于函数进行复合操作,所以可以利用输入层把$x$映射到$\phi(x)$ ,得到更加明显的特征,之后再把输出交给下一层
- 如果是二分类问题,最后一层只需要一个神经元即可,激活函数可以设置为Logistic函数
- 如果是多分类问题,可以把最后一层设置为C个神经元用于输出每一个类别的神经网络,可以利用softmax函数作为激活函数
可以见得,通过神经网络层的连接情况可以进行不同函数的拟合从而完成各种操作

参数学习

利用交叉熵作为损失函数,并且利用正则化来限制模型能力从而保证泛化能力,同时利用梯度下降的方法进行参数的学习: 梯度下降法需要计算损失函数对参数的偏导数，如果通过链式法则逐一对每个参数进行求偏导比较低效．在神经网络的训练中经常使用反向传播算法来高效地计算梯度

反向传播算法

由于每一次对于一个矩阵计算梯度的时间复杂度比较大,所以为了减小时间复杂度,就需要使用反向传播算法计算梯度,下面介绍反向传播算法的公式的基本推导过程和结论矩阵求导参考: 矩阵求导
首先求解损失函数对于每一权重的偏导数:
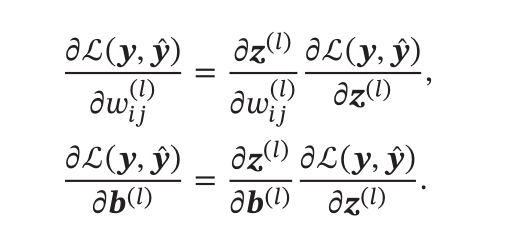
接下来只需要分别求解如下量即可 $$ \frac {\partial {z}^{(l)}} {\partial {\omega}_{ij}^{(l)}} 和 \frac {\partial {z}^{(l)}} {\partial {\mathbf b}^{(l)}} 和 \frac {\partial {\mathcal L}({\mathbf y},{\widehat {\mathbf y}})} {\partial {\mathbf z}^{(l)}} $$
计算方式如下(涉及到大量的矩阵运算)
接下拉计算误差 ${\sigma}^{(l)}$ 的传递规则:
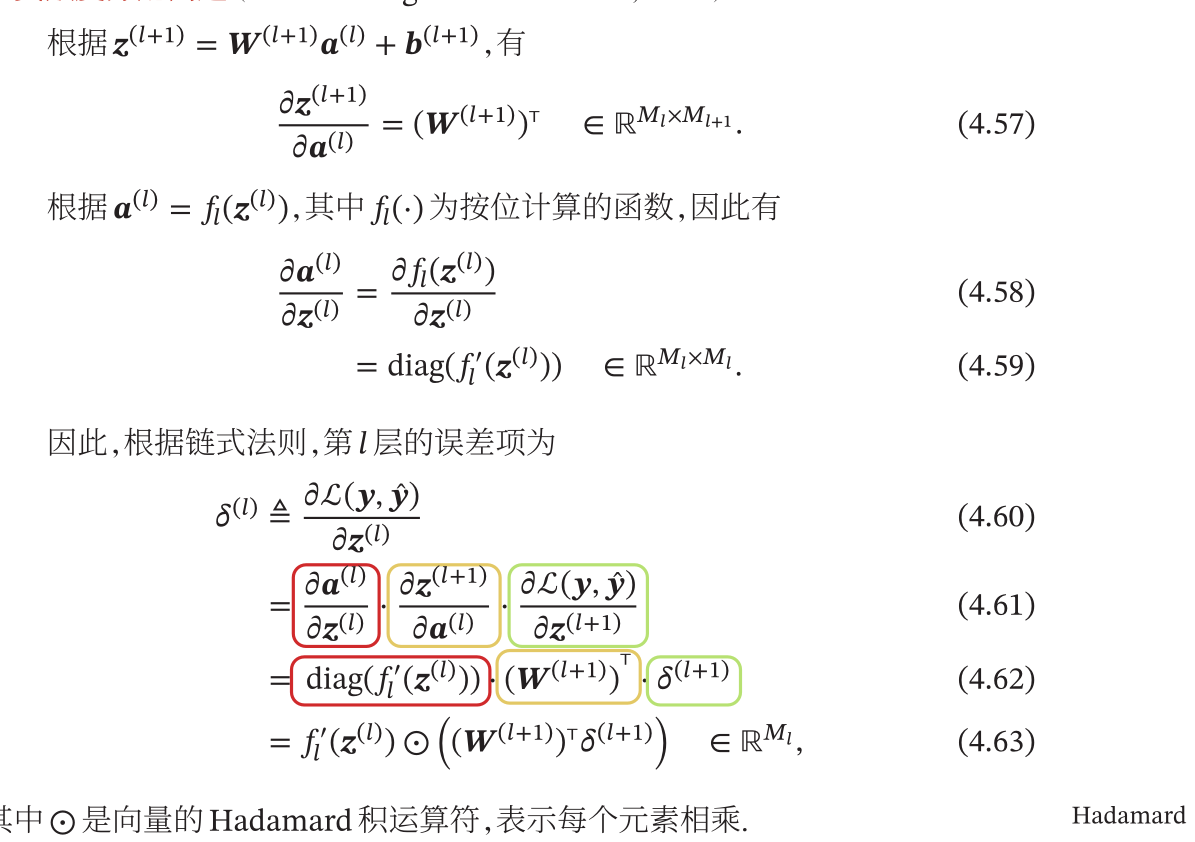
最终可以得到反向传播的结论:
通过上面的推导,误差可以使用递推公式进行计算,同时梯度可以转换为矩阵的计算,总体的计算方式如下:

自动梯度计算

三种方式: 数值计算(定义计算),符号计算(类似于按照各种不同的方式进行符号解析),自动微分
自动微分计算可以把函数拆分为各种运算符号和各种基本函数的结合,利用各种基本函数的微分求解方式来确定最终可以得到的偏导数,举例如下:
前向计算: 首先从h1开始计算向最终目标计算
反向计算: 从h6开始逐步积累
各种计算方式之间的关系

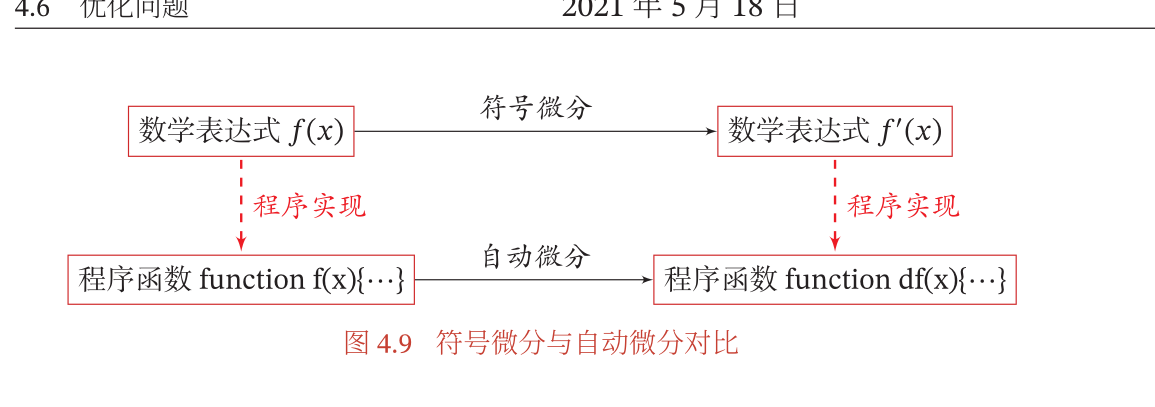
优化问题

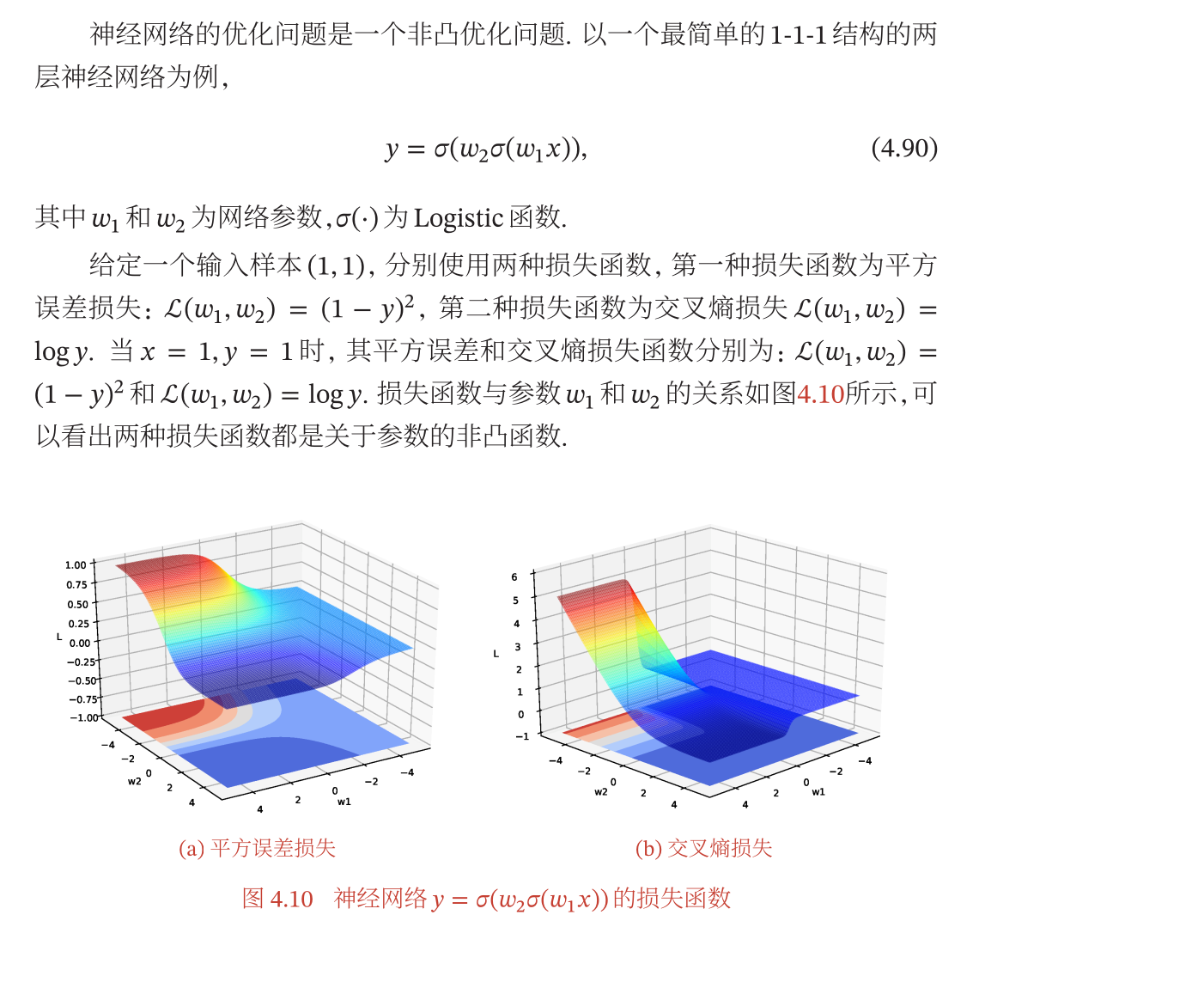
非凸优化问题

对于多层网络组成的复合函数,可能不是一个凸函数,那么就难以利用梯度下降找到最优解

梯度消失问题

对于误差传递公式:
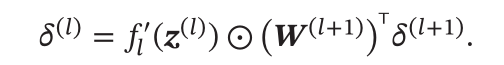
需要计算激活函数的导数,所以如果哪一个层的导数为0就会到时最终得到的结果中的梯度消失(回想反向传播公式中由误差项目)
但是对于一些激活函数,比如 $\sigma(x)$ 和 $tanh(x)$ 都是存在导数为0的点,所以都会导致梯度消失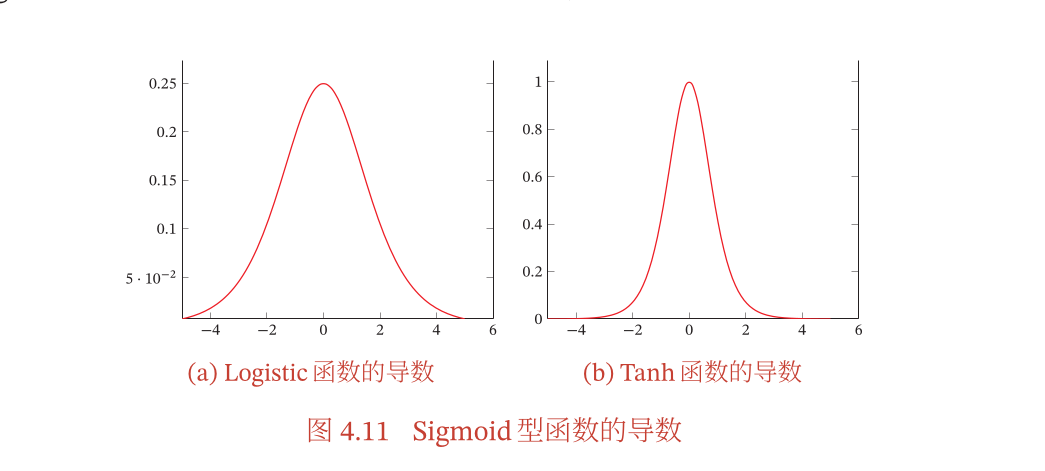

卷积神经网络

卷积的计算可以参考: https://zhuanlan.zhihu.com/p/268179286?ivk_sa=1024320u

卷积

我的理解卷积其实就是利用一组权重(可以是向量或者矩阵)从而对于输入的数据进行一系列的特征化得到新的数据的过程

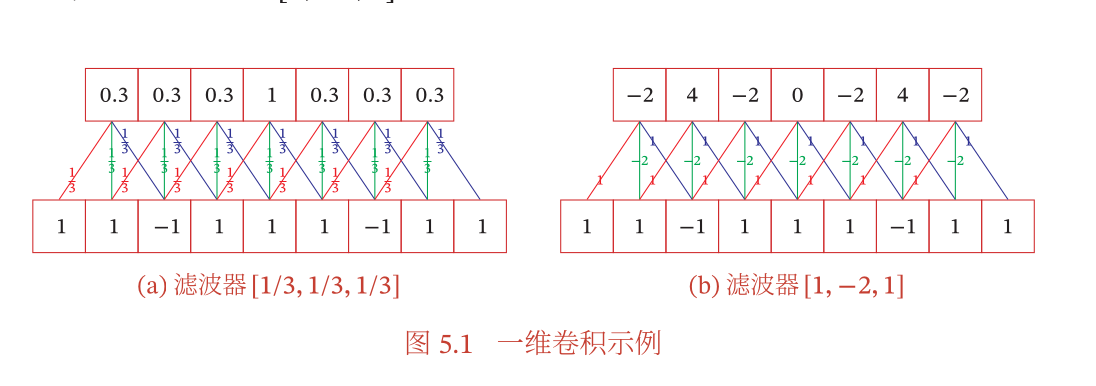
一维卷积

定义和距离如下:
一维卷积的图解(步长都是为1)

二维卷积

卷积核变成了一个矩阵,这一个矩阵用于表示一定范围内的元素的权重,可以用于计算权重和从而计算最终得到的矩阵中的元素,公式如下(看不懂...):
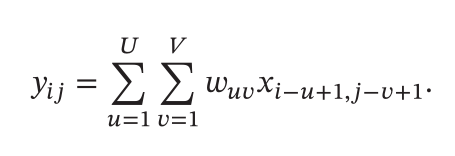
计算过程:
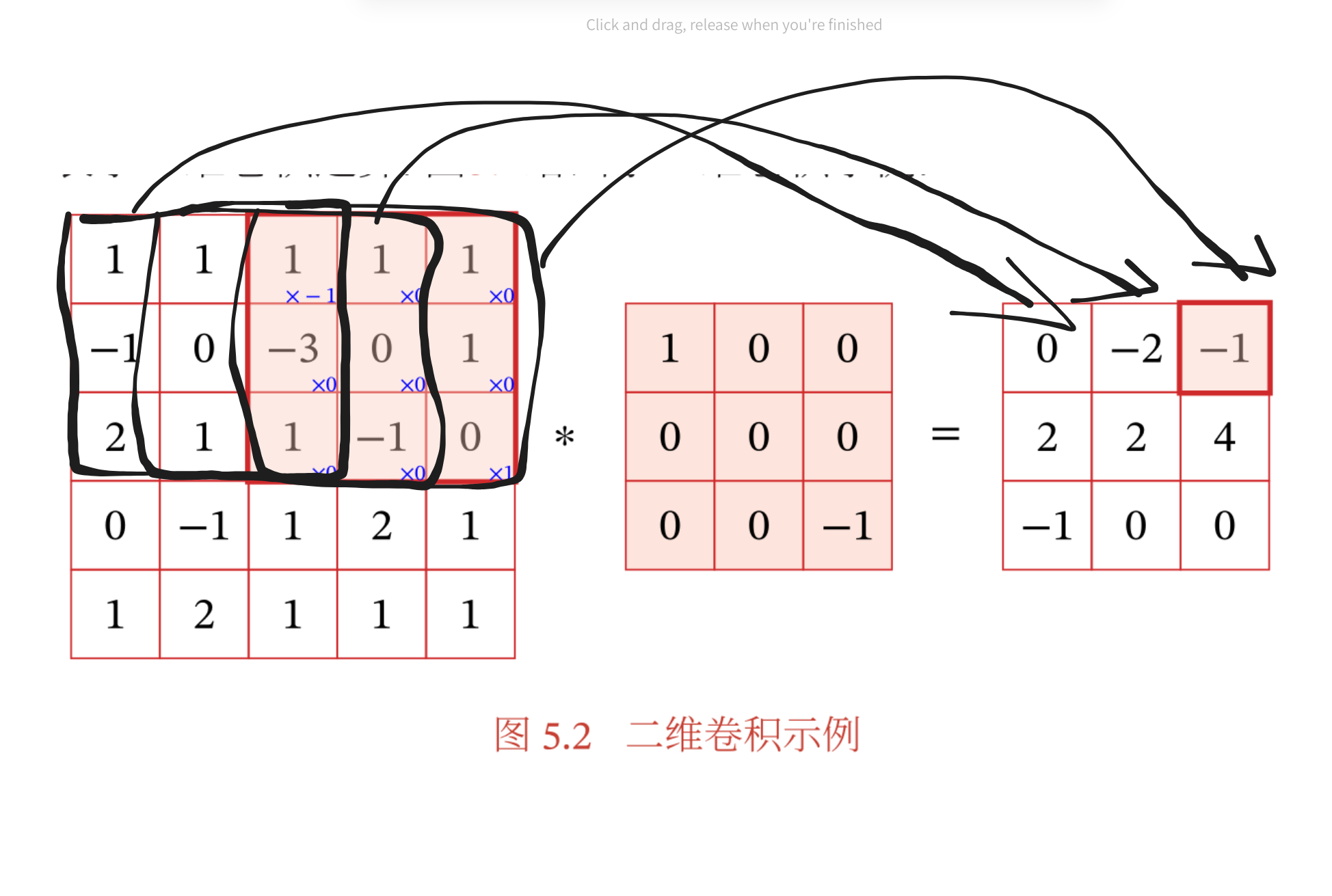
比如可以使用一个范围内的平均值来计算经过卷积之后的特殊值

互相关

也就是在利用卷积核的时候可以按照Hardmanda乘积的方式计算(也就是你想的那样),效果一样,变化公式如下: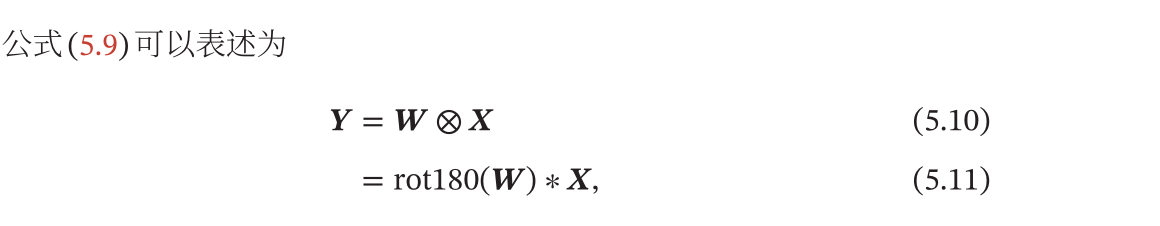

卷积的种类

注意步长就是卷积核每一次沿着样本滑动的距离,和卷积核本身无关,卷积的种类如下:

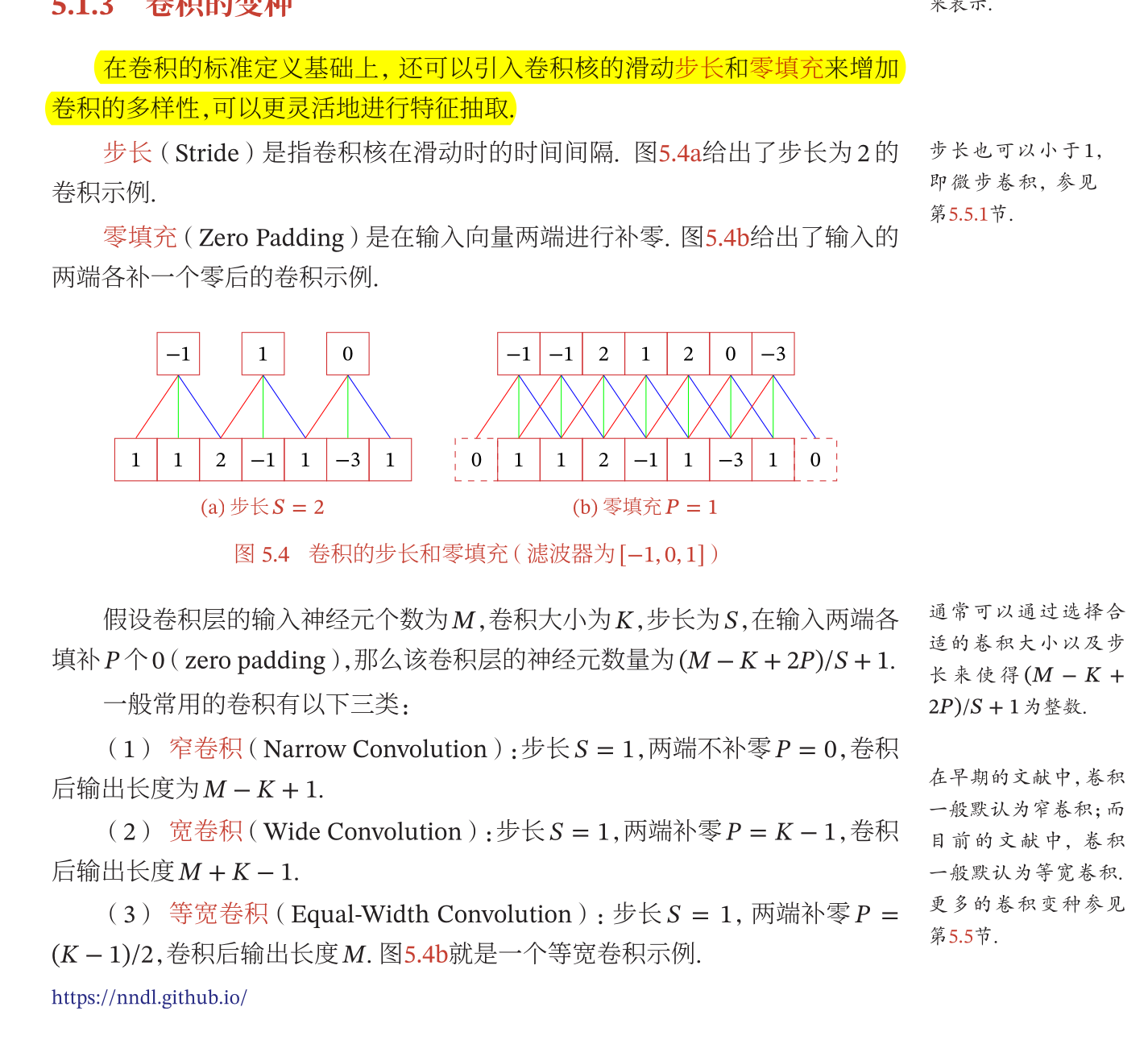
卷积的数学性质

交换性:
卷积的导数求解:

卷积神经网络(CNN)

卷积神经网络的特点

局部连接: 也就是在卷积层中每一个层的神经元都是只与前面的一部分神经元连接而不是和前面的神经元全连接,所以此时每一层的活性值(输出)与下一层的净输入量有如下的关系:
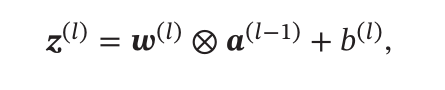
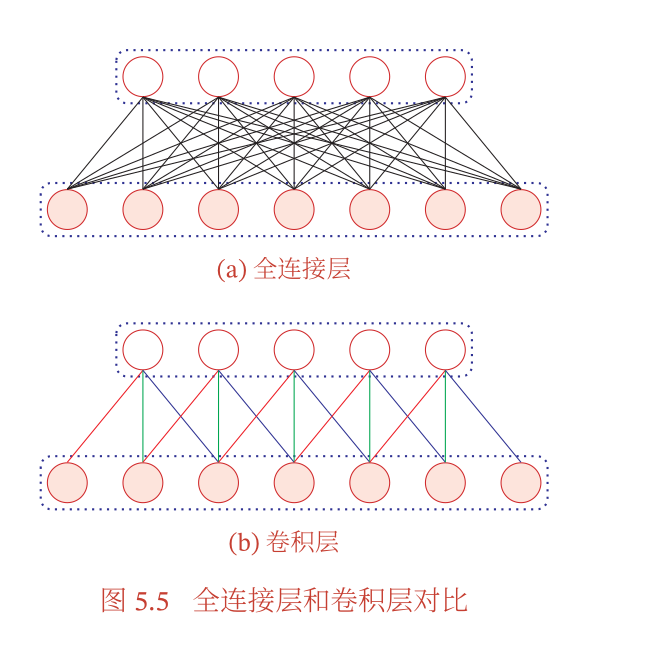
权重共享: 就是值得卷积核在输入特征的对应通道中扫描,所以所有被扫描到的部分都是共享同样一个权重的,也就是卷积核对应通道的权重

卷积神经网络的结构

注意卷积神经网络中神经元的连接是三维度的,比如对于一个图像,长和宽表示图像的分辨率,深度表示图像中的通道数量

卷积层

作用: 提取一个局部区域的特征,不同的卷积层相当于不同的特征提取器(比如一个用于提取颜色,一个用于提取轮廓等)
下面是对于输入特征映射组和输出特征映射组以及卷积核的阐述:
解释一下我比较困惑的几个点:
$X \in \mathbb R^{M \times N \times D}$ 表示输入是一个三维度的张量,可以类比为图片,M和N表示长和宽,D表示深度(通道数量)
$Y \in \mathbb R^{M' \times N' \times P}$ 表示输出也是一个三维度的张量,只不过这里把D个特征映射为了P个特征,这一个过程通过卷积操作
$\mathcal W \in \mathbb R^{U \times V \times P \times D}$ 首先U,V表示每一个权重矩阵的边长,P表示总共需要提取的特征个数(可以看成卷积层的层数),D表示每一个卷积核中权重矩阵的个数(也就是通道数量), $\mathcal W^{p,1}$ 表示用于提取第p个特征的第1个通道的权重矩阵

汇聚层(池化层)

作用类似于卷积层,作用也是用于提取特征,池化其实也是对于每一个区域进行一个下采样的过程(上采样表示把低维度的图片转换为高维度的图片)
一般就是把一个特征的某一个通道矩阵进行划分,并且利用划分区域中的特征来代表这一个区域的特征,常见的两种汇聚函数分为最大汇聚和平均汇聚(不用过多介绍了)
实际常常使用最大汇聚来实现下采样
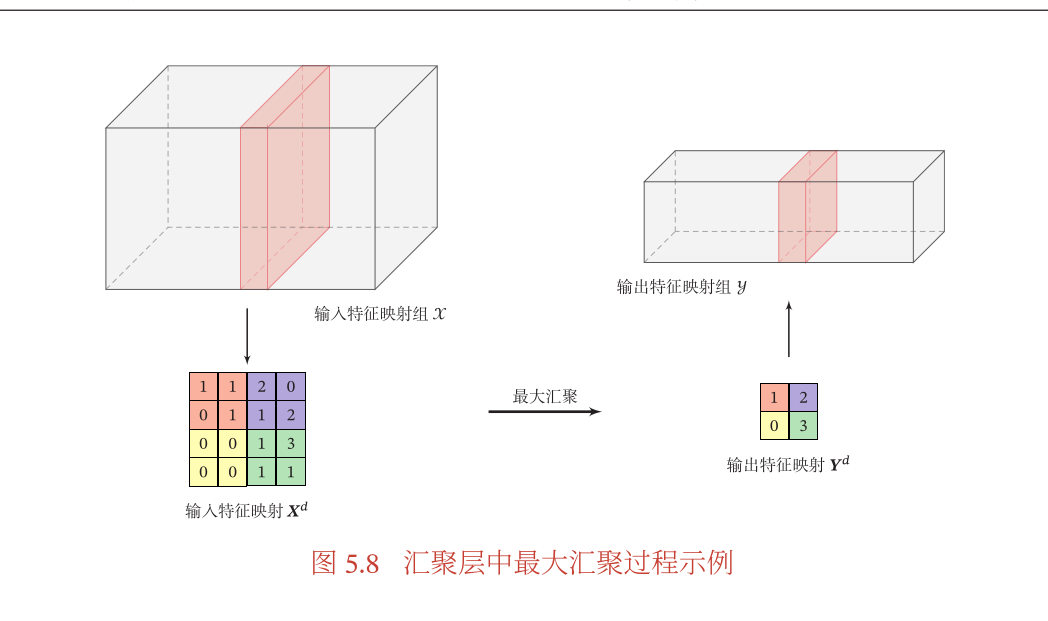
整体结构如下,注意卷积块可以更具需要提取特征的特殊来确定:

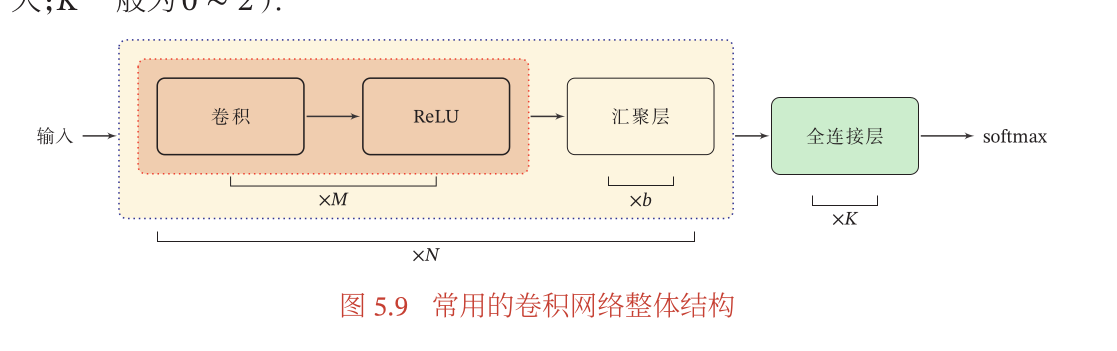
参数学习

梯度计算方式: 就是把点积换成卷积即可,其他的和全连接网络的计算方式一样:

CNN中的反向传播算法

误差反向传播算法在池化层和卷积层中不一样
在池化层中,误差传递公式和推导方式如下:
在卷积层中,误差传递公式如下(全连接网络中把乘积操作换成卷积操作即可)
需要注意如下事项:
- 卷积神经网络中的神经元分为三维度空间,用于采集比如图像一类的数据等
- 卷积操作和池化操作其实都是对于特征的提取,但是不同之处在与卷积操作需要利用卷积核(也就是具有对应通道个数的权重矩阵的集合)从而确定输出的特征图,但是池化只是对于输入图本身的一些操作,比如取平均值等
- 注意误差传递公式在池化层和卷积层中的应用
- 另外除了标准卷积还有很多卷积方式,同样标准卷积中神经元的个数可以通过公式计算

xzw'blog