这一次一定学会KMP算法

为什么要求解最长前缀

  • 首先什么是最长前缀:
    • 比如字符串为 $aabaaf$,那么索引范围为 $[0 , 4]$ 内的最长前缀就是$aa$
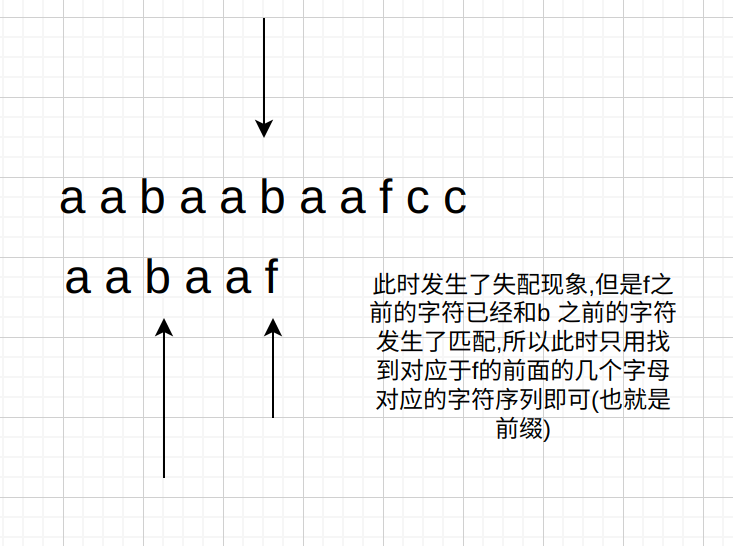
  • 最长前缀在字符串匹配中的含义: Pasted image 20241017181936.png
  • 前缀表的含义: $prefix[j]$ 表示索引范围为$[0,j]$ 的范围内最长前缀的长度大小,比如$aabaaf$的前缀表就是$0 1 0 1 2 0$
  • 另外注意前缀表还是最长的公共子字符串: 也就是说可以重复,比如$abcabcabc$ 的前缀表就是0 0 0 1 2 3 4 5 6,也就是abcabc可以充当最大公共前后缀,但是后面的讨论依然生效,只需要把不同的区域进行重合部分重合即可

next数组

  • next数组的作用就是指定如果在发生失配的时候,子字符串中的指针需要回退到哪一个位置,当然next可以就是前缀表,但是这样的化,比如j 的位置失配了,此时需要重新匹配的位置就是next[j - 1] 的位置,这样比较不方便,所以我这里采用的实现方式就是把前缀表中的数字减去$1$ 就可以得到next数组
  • 换而言之,$next[j]$ 表示字符串的索引范围为 $[0 , j]$ 的位置的最长前缀的最后一个字母的索引位置,比如字符串$aabaaf$的$next$ 数组也就是-1 0 -1 0 1 -1

next 数组的求解方式

  • 定义两个指针: i 指向当前遍历到的位置,j 指向索引范围为$[0 , i -1]$ 的前缀的最后一个字符,考虑如下两种情况
  • 如果$s[i] == s[j + 1]$ 那么说明,$i$ 的位置和前面的前缀匹配,所以此时需要把前缀表最后一个指针的位置向后面移动$1$ ,同时$next[i] = j$ ,这样就可以求解得到$next[i]$
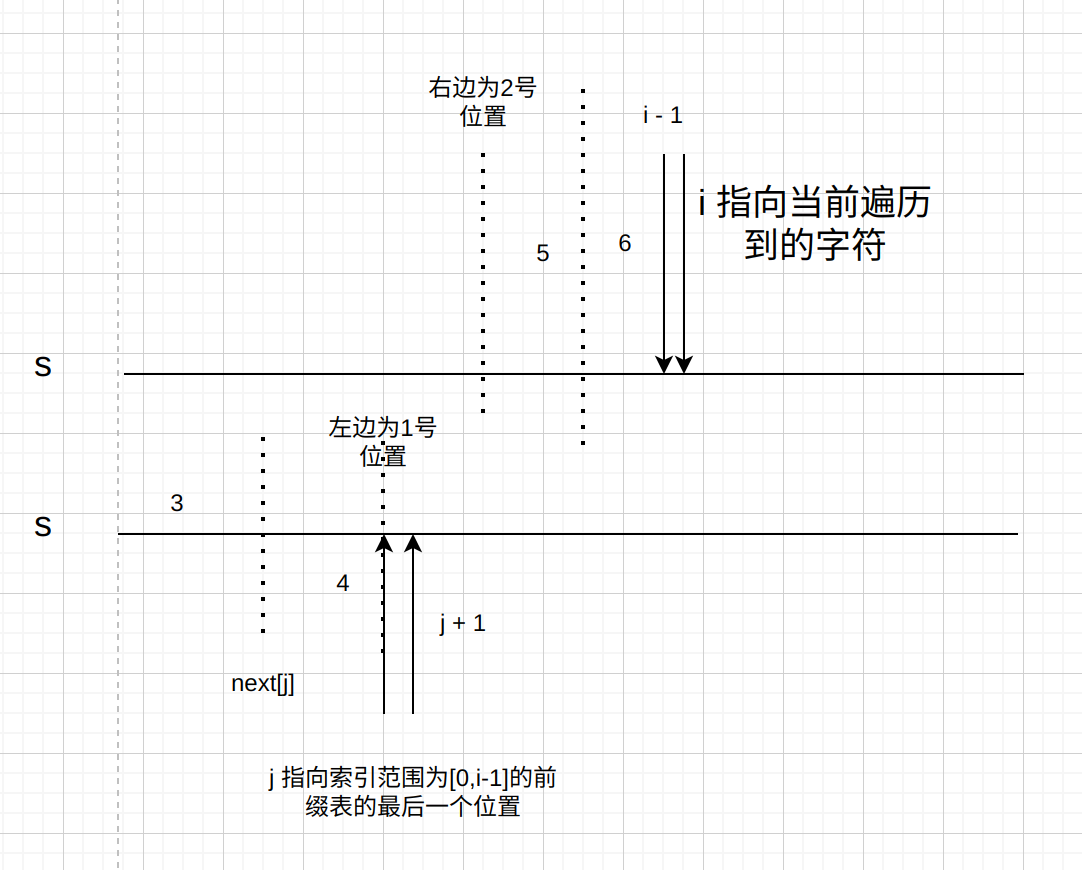
  • 如果$s[i] != s[j + 1]$ 那么此时就需要不断令$j = next[j]$ 知道二者相等或$j = -1$,这一种情况不太好理解,画图解释: Pasted image 20241017183847.png
  • 解释一下上图中,比如$s[j+1]!=s[i]$ ,==但是此时 $1$号位置和$2$号位置的字符串相同,并且对于$next[j]$ 左边的$3$ 号位置和右边的$4$ 号位置相同,由于$4$号位置和$6$号位置相同,所以$3$ 号位置和$6$号位置也相同==,所以此时可以利用$j = next[j]$ 进行回退
  • 所以求解Next数组的代码如下:
void getNext(vector<int>& next , string s) {
	int j = -1; // 表示最长前缀的最后一个字母的位置,也就是前缀的结尾
	next[0] = j;
	int i = 1; // 表示当前指向的字母,注意这一个字母的前面 (j + 1) 个字母都已经匹配了
	int n = s.size();
	for( ; i < n ; i ++) {
	while(j >= 0 && s[i] != s[j + 1]) {
		j = next[j];
	} 
	if(s[i] == s[j + 1]) {
		j ++;
	}
	next[i] = j;
	}
}

匹配过程

  • 终于到了匹配过程,匹配过程中比较重要的一点就是主字符串中的指针不移动,一直都是子字符串中的指针移动
  • 匹配过程中明确两个指针的含义: i 表示此时遍历到主字符串中的哪一个字符了,也就是当前字符的索引,j 表示i 前面已经匹配的最后一个字符的索引位置,这样做也是为了直接使用next[j]进行回溯
  • 还是考虑两种情况:
    • s[i] == t[j + 1] 此时匹配成功,j ++即可
    • s[i] != t[j + 1] 此时匹配失败,需要回退指针j = next[j] (具体原因看上面的图解)
  • 最后匹配的代码如下:
int kmpMatch(string& s , string& t) {
	vector<int> next(t.size() , 0);
	getNext(next , t);
	// j 指向 t 中已经匹配的最后一个字母 , i 表示 s 的当前字母
	int j = -1 , i = 0;
	for( ; i < s.size() ; i ++) {
		while(j >= 0 && s[i] != t[j + 1]) {
			j = next[j];
		}
		if(s[i] == t[j + 1]) {
			j ++;
		}
		if(j == t.size() - 1) return i - j; // 注意在循环中
	}
	return -1;
}

参考题目: https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/description/ https://leetcode.cn/problems/repeated-substring-pattern/