矩阵操作一定需要注意边界条件和变化公式等
- 矩阵置0:
- 空间复杂度为
O(m + n): 准备两个unordered_set放入需要置为0的行和列之后把这些行和列相应的位置置为0即可 - 空间复杂度为
O(1): 利用两个辅助变量,分别记录第一行或者第一列是是否需要置为0,之后在遍历的过程中如果遇到需要置为0的位置就可以直接令martix[i][0] = martix[0][j] = 0即可,最后遍历矩阵把需要置0的位置置为0
- 空间复杂度为
- 螺旋矩阵 模板挺多的,感觉最简单的模板是: 记录矩阵中的数字个数 + 转圈,利用四个变量记录边界位置即可
- 矩阵旋转 本质就是矩阵变化,两种方法:
- 利用辅助变量来进行矩阵的逆转: 矩阵旋转的变化公式为(注意观察一个数字的变化): $$ matrix[row][col] -> matrix[col][n - 1 - row] $$ 此时可以利用一个临时变量记录边界位置: $$ temp = matrix[row][col] $$
- 接下来确定 哪一个位置旋转到
matrxi[row][col](上面一个式子的逆变化) $$ matrix[row][col] = matrix[n - 1 - col][row] $$ 持续变化: $$ matrix[n - 1 - col][row] = matrix[n - 1 - row][n - 1 - col] $$ $$ matrix[n - 1 - row][n - 1 - col] = matrix[col][n - 1 - row] $$ $$ matrix[col][n - 1 - row] = matrix[row][col] = temp $$ 此时就构成了一个循环,不断进行上述的操作即可(奇数 or 偶数) - 同时需要确定开始区域,开始区域如下:
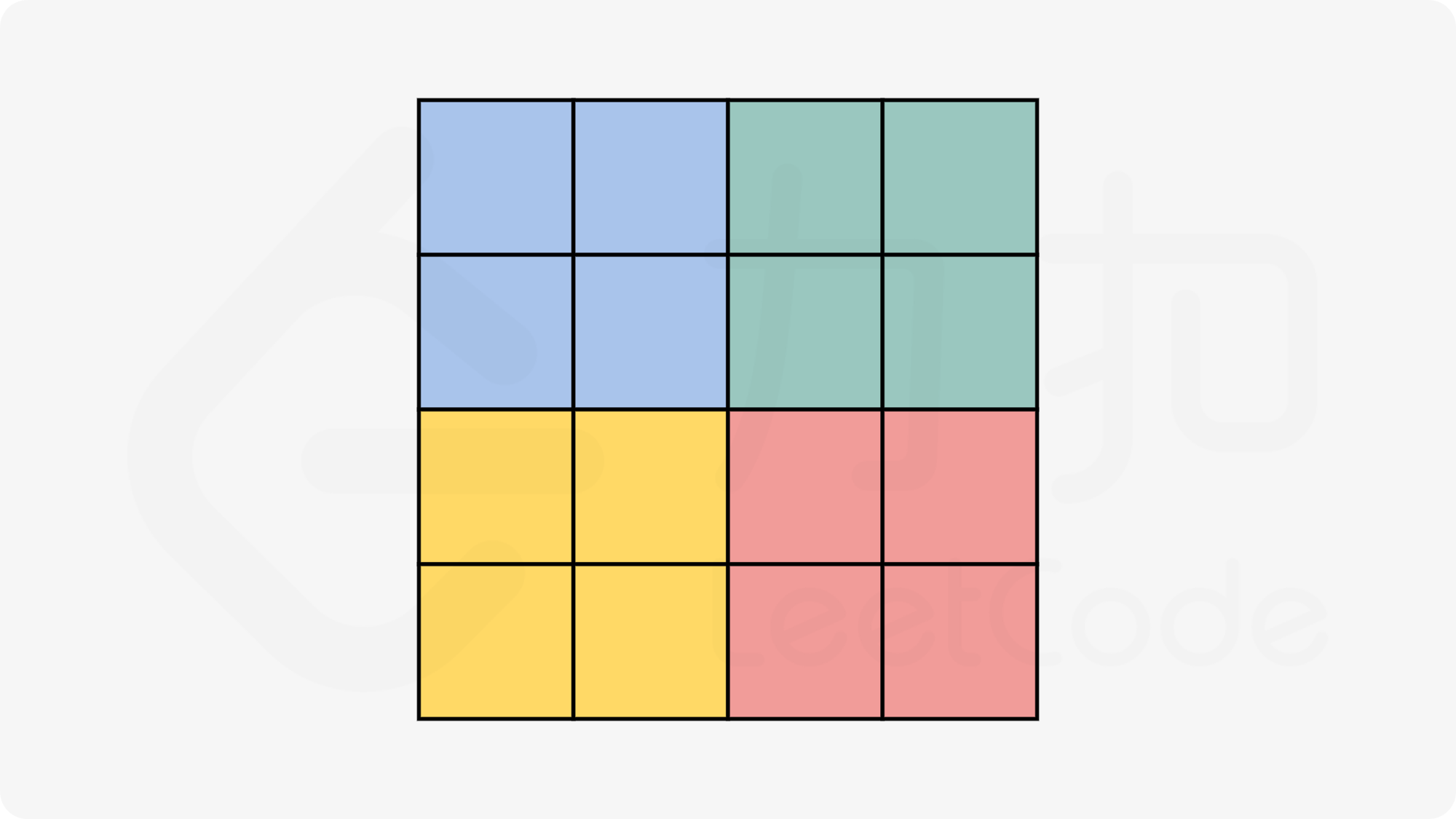
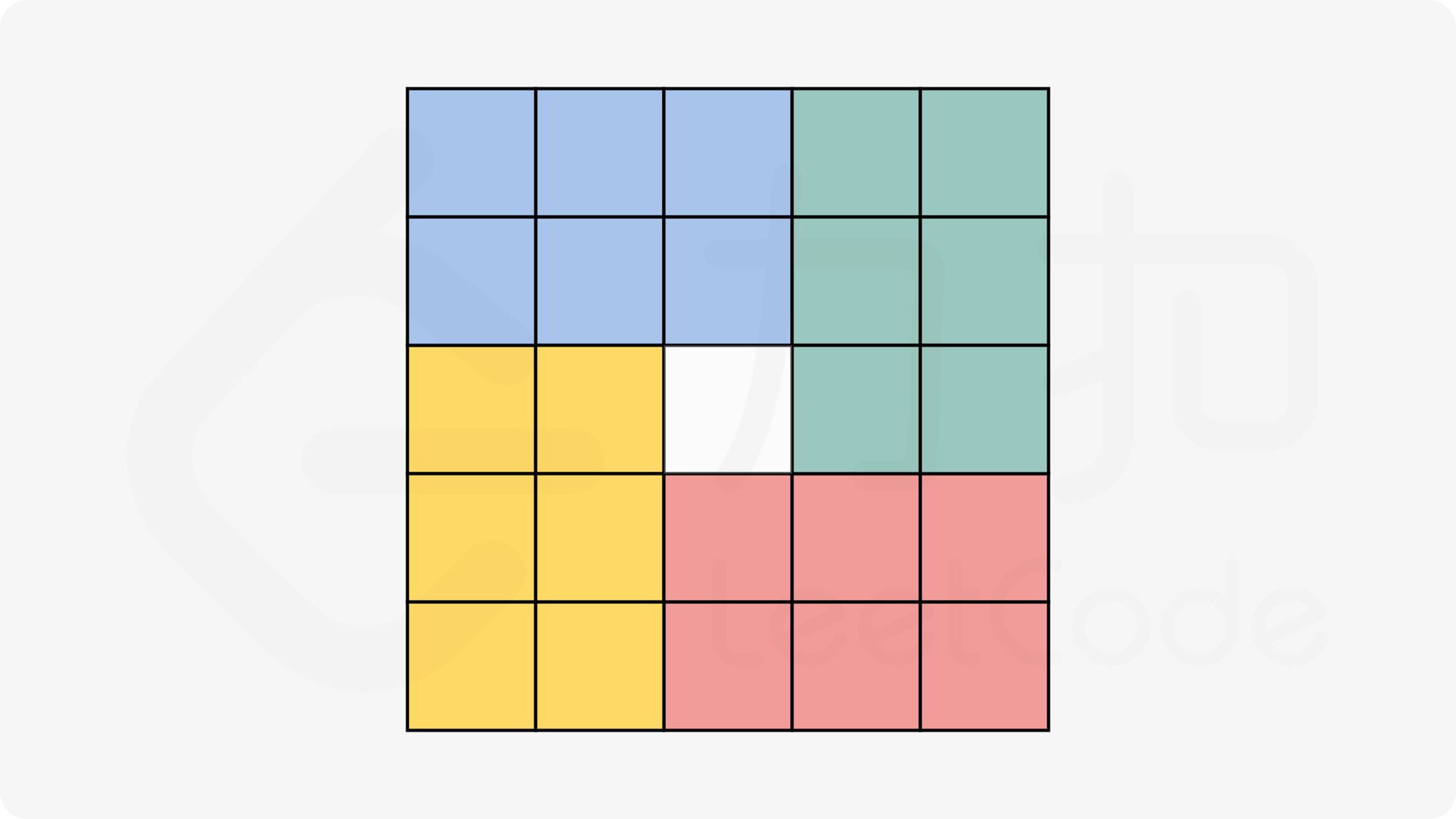
- 第二种方法: 矩阵变化,首先水平翻转之后转置即可: $$ 水平翻转: matrix[row][col] -> matrxi[n - 1 - row][col] $$
$$ 转置: matrix[row][col] -> matrix[col][row] $$ 所以进行复合变化可以得到: $$ matrix[row][col] -> matrix[col][n - 1 - row] $$ 刚好得到矩阵的旋转公式 4.二维矩阵搜索 把矩阵看成一个二叉搜索树即可,可以把左下节点或者右上节点当成开始节点,那么就可以得到:
- 如果
matrix[i][j] < target -> j ++ - 如果
matrix[i][j] > target -> i --即可,最终不断搜索就可以找到目标节点