1. 寻找正序数组中的中位数
基本思路
这里的基本思路就是进行数组分组,比如假设第一个数组(假设为 A)的长度为 m , 第二个数组(假设为 B)的长度为 n , 那么两个数组中总共的元素个数为 m + n 个, 所以此时需要在 A 中划分出 i 个元素进入到集合a 中,并且在B 中划分 j个元素进入集合 a 中,其他的元素进入集合 b 中,并且使得如下条件满足就可以找到中位数:
$$
\begin{equation} size(a) = i + j =\left{ \begin{aligned} \frac{m+n}{2} (m + n 为偶数) \ \frac{m+n+1}{2}(m+n为奇数) \end{aligned} \right. \end{equation}
$$
并且同时有:
$$
max(a) <= min(b)
$$
举例,对于任意的 i 和 j , 遍历过程中之需要下面的式子成立即可(图解如下):
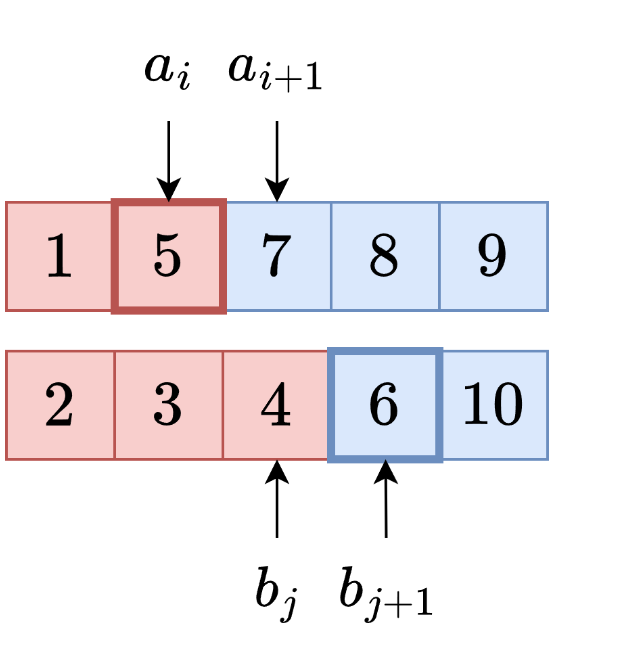 要使得上面的条件成立,那么也就是如下的推导成立:
$$
max(a_i,b_j) \leq min(a_{i + 1} , b_{j + 1})
$$
$$
由于 a_i \leq a_{i + 1} 并且 b_j \leq b{j + 1} 成立,所以之需要如下式子成立:
$$
$$
a_i \leq b_{j + 1} 并且 b_j \leq a_{i + 1} 成立
$$
如果考虑在头部和尾部的位置,分别添加上无穷大,那么根据两个数列的趋势线,最后一定会有交点,图解如下(所以存在性得证!):
要使得上面的条件成立,那么也就是如下的推导成立:
$$
max(a_i,b_j) \leq min(a_{i + 1} , b_{j + 1})
$$
$$
由于 a_i \leq a_{i + 1} 并且 b_j \leq b{j + 1} 成立,所以之需要如下式子成立:
$$
$$
a_i \leq b_{j + 1} 并且 b_j \leq a_{i + 1} 成立
$$
如果考虑在头部和尾部的位置,分别添加上无穷大,那么根据两个数列的趋势线,最后一定会有交点,图解如下(所以存在性得证!):
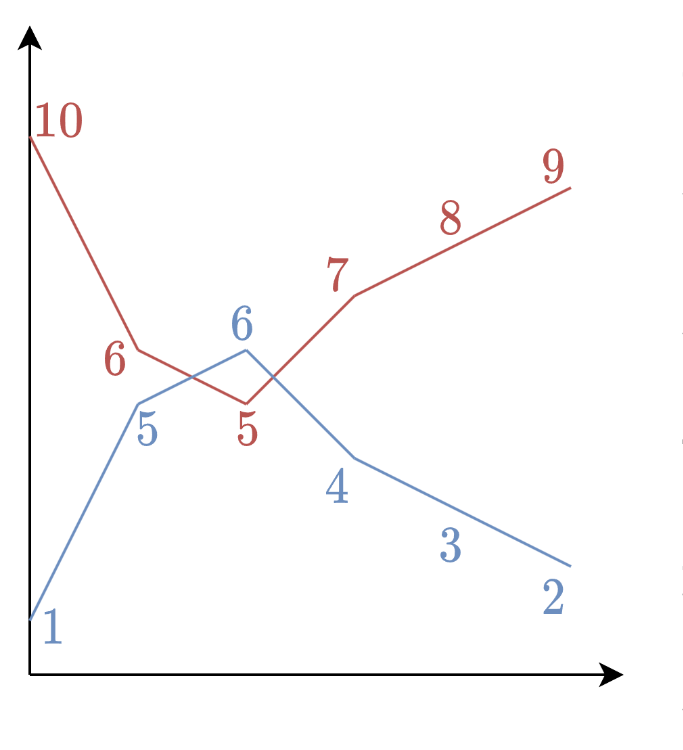 同时由于 $a_{i + 1} > b_j$ 所以在之后的数组中,$a_{i + 1}$ 进入第一组,所以在之后的枚举中,第一组中的 $a_{i + 1}$ 已经大于了第二组中的 $b_j$ 了,所以不满足条件,并且由于 $a_i < b_{j + 1}$ 之前的枚举也是一样的不满足条件所以唯一性得证!
同时由于 $a_{i + 1} > b_j$ 所以在之后的数组中,$a_{i + 1}$ 进入第一组,所以在之后的枚举中,第一组中的 $a_{i + 1}$ 已经大于了第二组中的 $b_j$ 了,所以不满足条件,并且由于 $a_i < b_{j + 1}$ 之前的枚举也是一样的不满足条件所以唯一性得证!
解题方法
为了方便处理边界,也就是一定需要让两个数组产生交点,可以在第一个数组前面添加一个 负无穷, 并且在第二个数组后面添加一个正无穷大 ,同时为了方便只是移动 第一个数组中的指针,可以令 $sizeof(a) \leq sizeof(b)$ 成立即可,同时 $i$ 表示数组 $a$ 中的在第一组中的元素的个数,$j$ 表示数组$b$ 中的在第一个元素中的元素,同时初始位置需要满足 $i = 0 并且 j = \lfloor \frac{m + n + 1}{2} \rfloor$ , 同时对于结果的处理如下, 如果 $m + n$ 为偶数,那么答案就是 $max(a_i,b_j) 和 min(a_{i + 1} , b_{j + 1})$ 的平均值,如果 $m + n$ 为奇数,那么中位数就是 $max(a_i,b_j)$ ,所以这里可以使用枚举法求解,代码比较简单
二分优化
二分查找不仅仅是一种根据元素大小进行查找的算法,同时可以根据条件查找,这里可以利用二分查找寻找 $i$ 的位置,使得上面的条件满足(可以理解为二分查找的要求就是$mid$ 前面或者后面的元素一定满足要求即可): $$ a_i \leq b_{j + 1} 并且 b_j \leq a_{i + 1} $$ 并且这样的 $i$ 只有一个,同时 $i 和 j$ 之间满足特定的关系,所以可以使用二分查找来搜索 $i$ 的位置,这里我习惯使用闭区间的方式,所以初始化方法如下:
int left = 0;
int right = a.size() - 1;
int i = (left + right) / 2;
// i 和 j 为下标,所以元素个数为 i + 1 + j + 1 = (m + n + 1) / 2
int j = (m + n + 1) / 2 - i - 2;
并且注意到最终 $left = right$ 的时候刚好是临界条件,所以此时 $left$ 移动打破临界条件,所以此时求解得到的 $i = right = left - 1$ 成立(二分查找基本都是这样的),所以最终求解结果的代码如下(注意头尾情况):
int i = left - 1;
int j = (m + n + 1) / 2 - i - 2;
int ai = i >= 0 ? nums1[i]: INT_MIN;
int bj = j >= 0 ? nums2[j]: INT_MIN;
int ai1 = i + 1 < m ? nums1[i + 1]: INT_MAX;
int ai2 = j + 1 < n ? nums1[j + 1]: INT_MAX;
int max1 = max(ai,bj);
int min2 = min(ai1 , bj1);
return (m + n) % 2 == 0 ? (max1 + min2) / 2 : max1;
2. 最长有效括号
动态规划
- 这里只是针对于
s[i] == )的情况,在这一个情况下,dp数组的含义如下:dp[i]表示以i结尾位置的连续有效括号数量
- 递推公式如下:
- 如果
s[i - 1] == (那么此时就有dp[i] = dp[i - 2] + 2 - 如果
s[i - 1] == ),那么此时就有dp[i] = dp[i - 1] + dp[i - dp[i - 1] - 2] + 2推导过程如下图: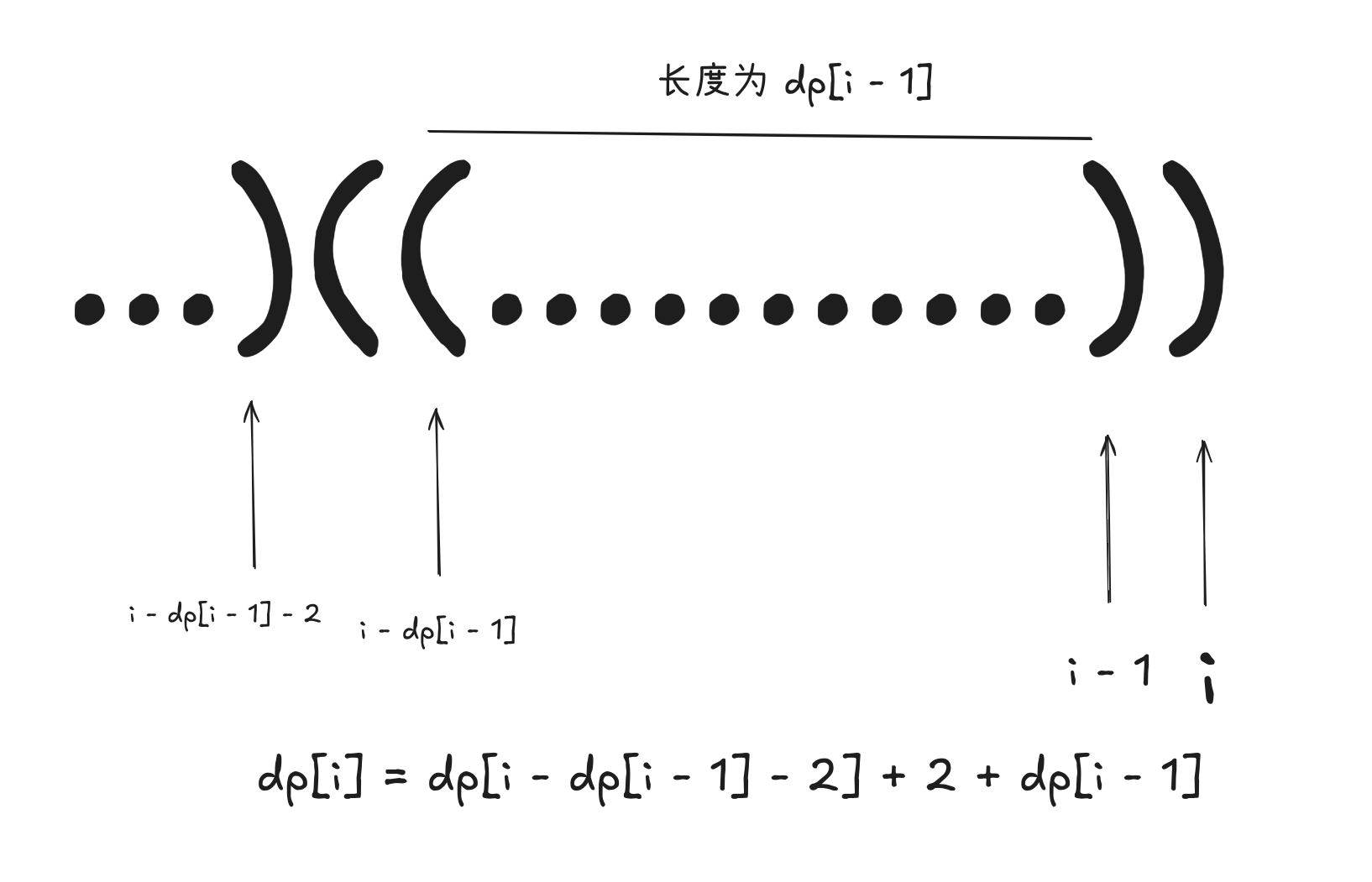
- 如果
栈
还是动态规划好理解,利用栈的思想就是首先如果是 ( 那么就需要压入下标到栈中,并且在栈中压入 -1 , 对于 ) 首先弹栈,如果栈为空那么就需要压入当前下标到栈中,否则就可以更新最大值了: ans = max(ans , i - st.top())
3. 正则匹配
动态规划: dp[i][j] 表示长度为 i 和 j 的两个字符串子串是否匹配,需要分情况讨论,下面画图分析,注意理解 *是重复前面的字符,并且不会去掉自己
第一种情况: p[j - 1] == s[i - 1] || p[j - 1] == . :
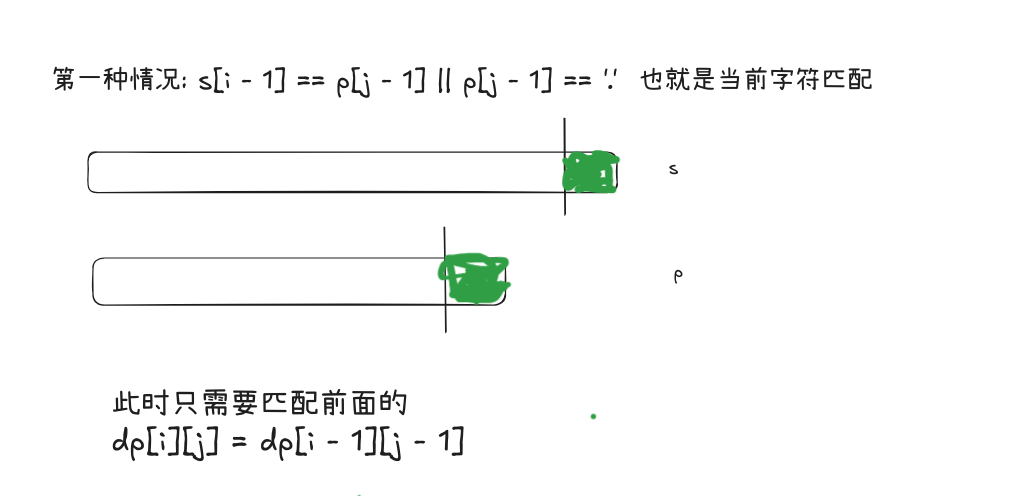
第二种情况不匹配但是, p[j - 1] == * , 那么又可以分为两种情况讨论,图解如下:
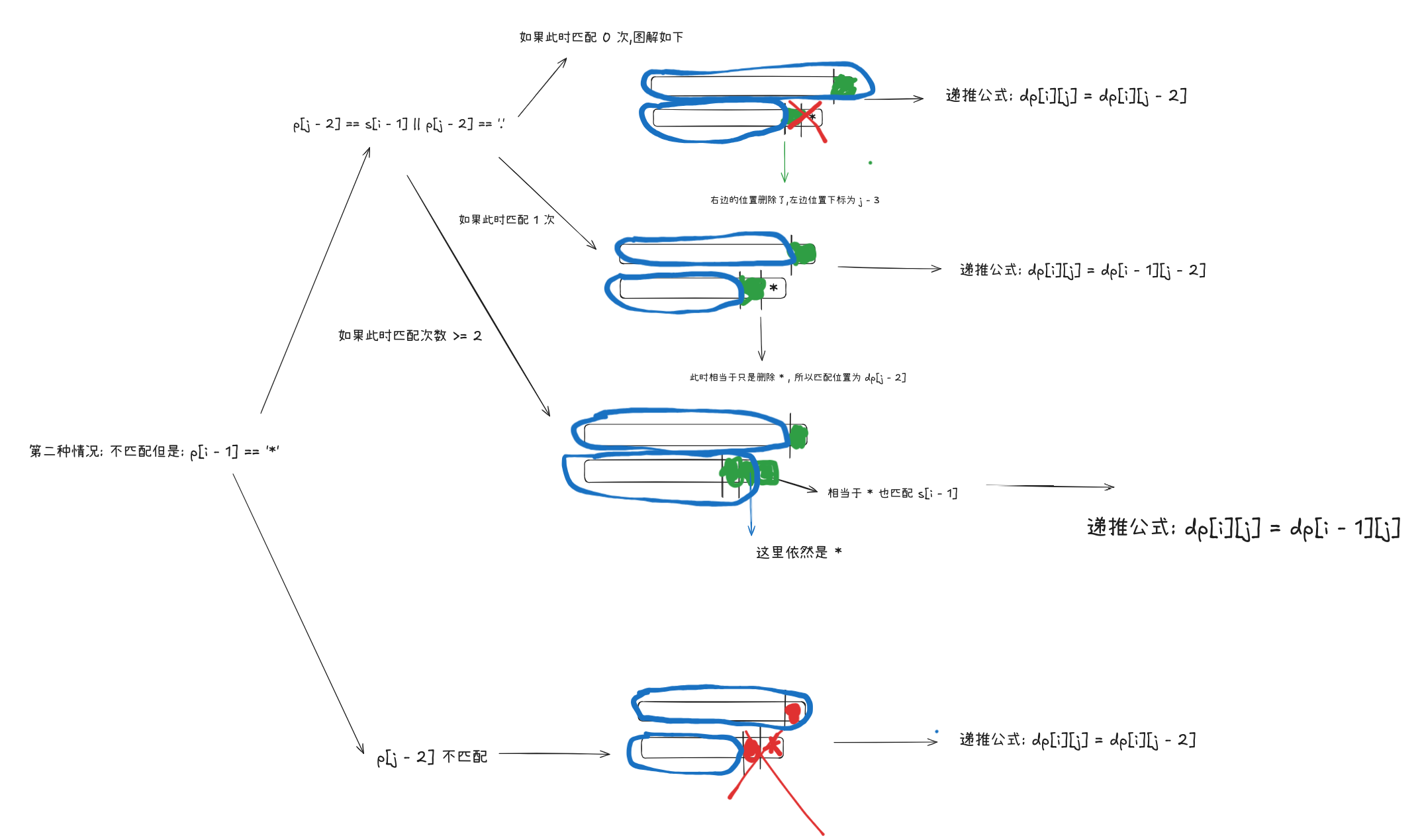
4. 串联所有单词的子串
滑动窗口问题,这里是定长的滑动窗口,类似于 找到所有字母异位词语
区别就是那一道题目是非定长滑动窗口,这一道题目是定长滑动窗口,关键在与窗口的划分,利用哈希表(std::pmr::unordered_map)统计词频率即可,图解如下:
