强化学习中的概念
-
状态(
state): 表示当前所处的环境 -
行为(
Action): 表示智能体可以作出的动作 -
智能体(
Agent): 表示可以作出动作的实物 -
策略(
policy): 也就是 $\pi$ 函数,也是强化学习的目标 $\pi(a | s) = \mathbb P(A = a| S = s)$ ,也就是根据各种行为的条件概率来确定下一步需要采取的动作 -
奖励(
reward): 表示采取相关的行为之后就会得到相应的奖励 -
状态转义(
state transition): 从一个状态转移到另外一个状态 $p(s^{'}|s,a) = \mathbb P(S^{'}|S = s,A = a)$ -
交互方式:

-
注意随机性:
- 根据策略函数 $\pi(a|s)$ 会根据环境随机得到下一步动作
- 根据状态转义函数 $\mathbb P(S^{'}|S ,a)$ 会随机进入下一个环境
-
轨迹: $s_1 -> a_1 -> r_1 -> s_2 -> a_2 -> r_2 ... s_T -> a_T -> r_T$
-
回报(
Return): 表示从当前时刻开始的奖励一致累积加到游戏的最后时刻的奖励之和,也就是: $U_t = R_t + R_{t + 1} + R_{t + 2} + R_{t + 3} + ...$ -
折扣回报(
Discounted): 这是由于当前的奖励的权重需要大于之后奖励的权重,所以定义折扣回报: $U_t = R_t + \gamma R_{t + 1} + {\gamma}^2 R_{t + 2} + {\gamma}^3 R_{t + 3} + ...$ (折扣率是超参数) -
给定环境,回报依赖于随机变量: $A_t , A_{t + 1} , A_{t + 2} , A_{t + 3} ...$ 和 $S_t , S_{t + 1} , S_{t + 2} , S_{t + 3} ...$
-
动作价值函数: 由于强化学习的目标是让当前的回报最大,所以引入了动作价值函数的概念: $$ Q_{\pi}(s_t,a_t) = \mathbb E[U_t | S_t = s_t , A_t = a_t] $$
-
动作价值函数反映了,当前环境$s_t$下采取$a_t$动作,产生的回报的均值,也就是随机变量是 $A_{t + 1} , A_{t + 2} ...$ 和 $S_{t + 1} ,S_{t + 2}...$ 定义 $Q^$函数如下 $$ Q^(s_t,a_t) = max_{\pi}Q_{\pi}(s_t,a_t) $$
-
状态价值函数: 反映了当前环境 $s_t$下采取不同行为的动作价值函数的均值: $$ V_{\pi}(s_t) = \mathbb E_A[Q_{\pi}(s_t,A)] = \sum\limits_a{\pi}(a|s_t)Q_{\pi}(s_t,a_t) $$
-
如果动作是连续的,就可以利用如下公式: $$ V_{\pi}(s_t) = \mathbb E_A[Q_{\pi}(s_t,A)] = \int{\pi}(a_t|s_t) Q_{\pi}(s_t,a_t) da $$
-
强化学习的过程:
- 学习策略: $\pi(a_t|s_t)$ (对于策略,输入环境即可得到动作$a_t$ )
- 学习动作价值函数: $Q_{\pi}^*(s_t | a_t)$ (选出最好的动作)
-
gym是类似于强化学习的训练集,也就是可以利用gym类似于环境,可以利用其中的环境
价值学习
- 目标近似 $Q^(s,a)$ , 当前需要采取的动作就是 $a = argmax_aQ^(s,a)$
DQN: 利用一个神经网络来近似与 $Q^*(s,a)$ 函数,只要训练次数足够多就可以使得足够近似- 利用
DQN进行强化学习的过程如下: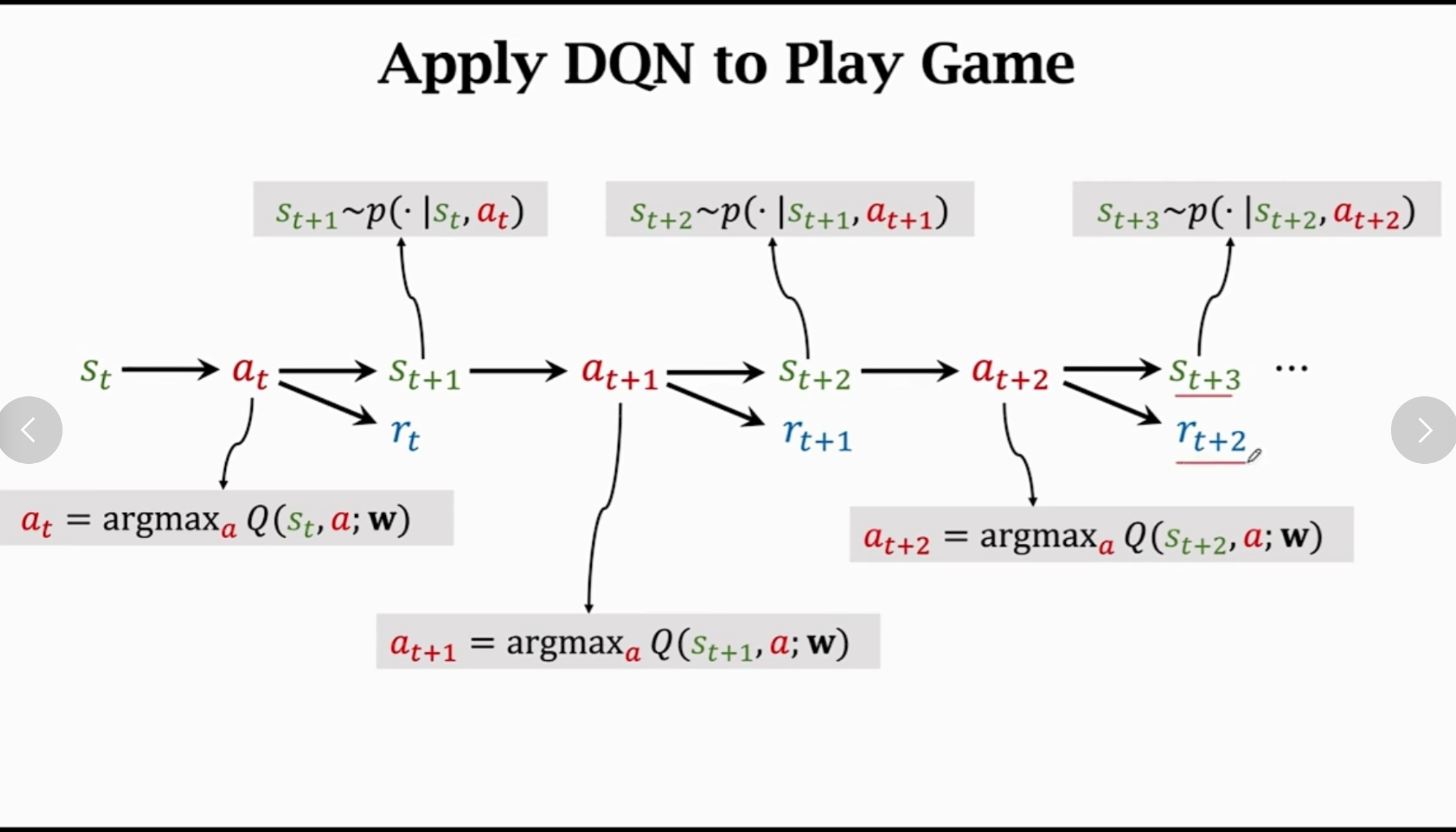
TD算法: 需要每一次完成一个动作,估计实际的收益和预测的收益,利用损失函数求解梯度,从而利用梯度下降从而更新模型参数,实际上也是一种深度学习算法,通过学习$Q^*$ 函数从而求解参数- 深度强化学习中: $$ Q(s_t,a_t;\mathbf w) = r_t + \gamma Q(s_{t + 1},a_{t + 1};\mathbf w) $$
- 利用这一个关系就可以进行递推公式,所以可以利用如下的关系式来确定参数
- 下图中的
TD target表示表示实际值,通过与预测值求解损失函数的方法确定下降梯度:
策略学习
- 利用神经网络来近似策略函数 $\pi(a|s)$ 输入状态 $s$ 输出动作 $a$
- 利用神经网络来确定策略网络 $\pi(a | s;\mathbf \theta)$ ,可以利用
softmax最后得到一个分布列 - 主要是对于状态价值方程:
- 算法的工作流程:

- 其中计算 $q_t = Q_{\pi}(s_t,a_t)$ :
- 可以利用一个整个过程,对于这一个过程直接计算 $Q_{\pi}(s_t,a_t)$ 也就是 $E[U_t]$ 即可
- 另外一种方法就是利用神经网络近似
- 神经网络需要预测的策略函数可以写成: $$ V(s;\mathbf \theta) = \sum_a{\pi}(a|s;\mathbb \theta)Q_{\pi}(s,a) $$
- 利用梯度上升函数即可计算: $$ \mathbf \theta = \mathbf \theta + \frac {\partial V(s;\mathbf \theta)} {\partial \mathbf \theta} $$
- 两种导数形式如下:

Actor-Critic 方法
-
Actor策略网络(决定动作) -
Critic价值网络(评价动作) -
基本模型如下: $$ V_{\pi}(s) = \sum_a{\pi}(a|s)Q_{\pi}(s,a) = \sum_a{\pi}(a|s;\mathbf \theta) q(s,a;\mathbf \omega) $$
-
其中后面两个是利用神经网络近似得到的函数
-
策略网络: 输入状态,输出各种特征的概率,为了得到更大的回报
-
价值网络: 输入状态和动作,输出回报,从而使得评判更加精准
-
对于价值网络,可以使用
TD算法来训练,需要使得打分更加精准
-
利用策略梯度算法使得策略网络可以得到的回报更大

-
使用
Actor-Critic算法的步骤:
-
最后的 $q_t$ 也可以使用 $\delta _t$ ,最好使用后者
-
最后的目的是学习策略网络
实例(围棋游戏)
- 状态: 存储一个棋盘和上面的棋子,可以使用一个
tensor,大小为19*19*2 - 动作: 可以使用一个一维的
tensor记录为之即可,比如n表示放置到第n个位置
蒙特卡诺方法
- 表示利用随机变量来估计目标值: 比如利用随机变量估计$\pi$
- 近似求解积分:
$$ 对于 F(x) = \int_a^bf(x)dx 可以利用如下方法求解积分,在区间里面取得x_1,x_2...,求解 (b - a)\frac{1}{N}\sum f(x_i) 即可近似F(x) $$
Q-learning算法
- 用于求解 $Q^*(s_t,a_t)$
- 核心公式: $$ Q^(s_t,a_t) = \mathbb E[R_t + \gamma max_a Q^(S_{t + 1},a)] = r_t + \gamma max_aQ^*(s_{t + 1},a) $$
- 神经网络的
Q-learning算法: