xzw'blog

回溯算法的本质其实就是穷举法,回溯算法可以用于解决各种问题

• 回溯算法可以解决的问题如下:
  • 组合问题(N个数字里面找出K个数字的集合(部分顺序))
  • 切割问题(一个字符串的切割方式)
  • 子集问题(一个集合中有多少个符号要求的子集)
  • 排列问题(N个数字按照一定规律进行全排列总共的排列方案种类数)
  • 棋盘问题(比如N皇后等)
• 解决回溯算法的问题一定要列举状态图,也就是每一层递归之后选择的元素一定需要列出来
• 回溯算法的模板:

void backtracking(参数) {
	if(终止条件) {
		存放结果
		return ;
	}

	for(选择下一层的元素) {
		处理节点
		backtracking(路径,目标);
		回溯,撤销选择
	}
}

组合问题

1. 组合 组合问题的模板题,注意这里需要一个变量来控制但前的层数(也就是当前遍历节点的状态),这里使用一个Index进行遍历,[index + 1 , n] 表示这一个节点的下一层 代码: make_pair1.cpp 同时注意利用有效索引范围来进行减枝操作,注意最大有效索引的推导方式,减枝代码如下: make_pair2.cpp
2. 组合总和III 组合问题,需要一个startIndex来控制当前遍历到的行数,另外减枝操作,当当前遍历的startIndex向后面循环的时候如果遇到sum > target的情况就需要立刻返回(之后的数字都不满足要求了,注意return和continue的区别) 组合问题III.cpp
3. 电话号码的字符组合 还是一定需要注意递归的层数的表示方式,这里每一层其实就是每一个字符的集合,所以每一层中只需要遍历字符集合即可,所以递归的参数就是需要传入可以代表字符集合的控制量,这就是当前遍历到的索引值,一定需要明确每一层到底遍历的时什么,可以作状态图: 电话号码的字符组合.cpp
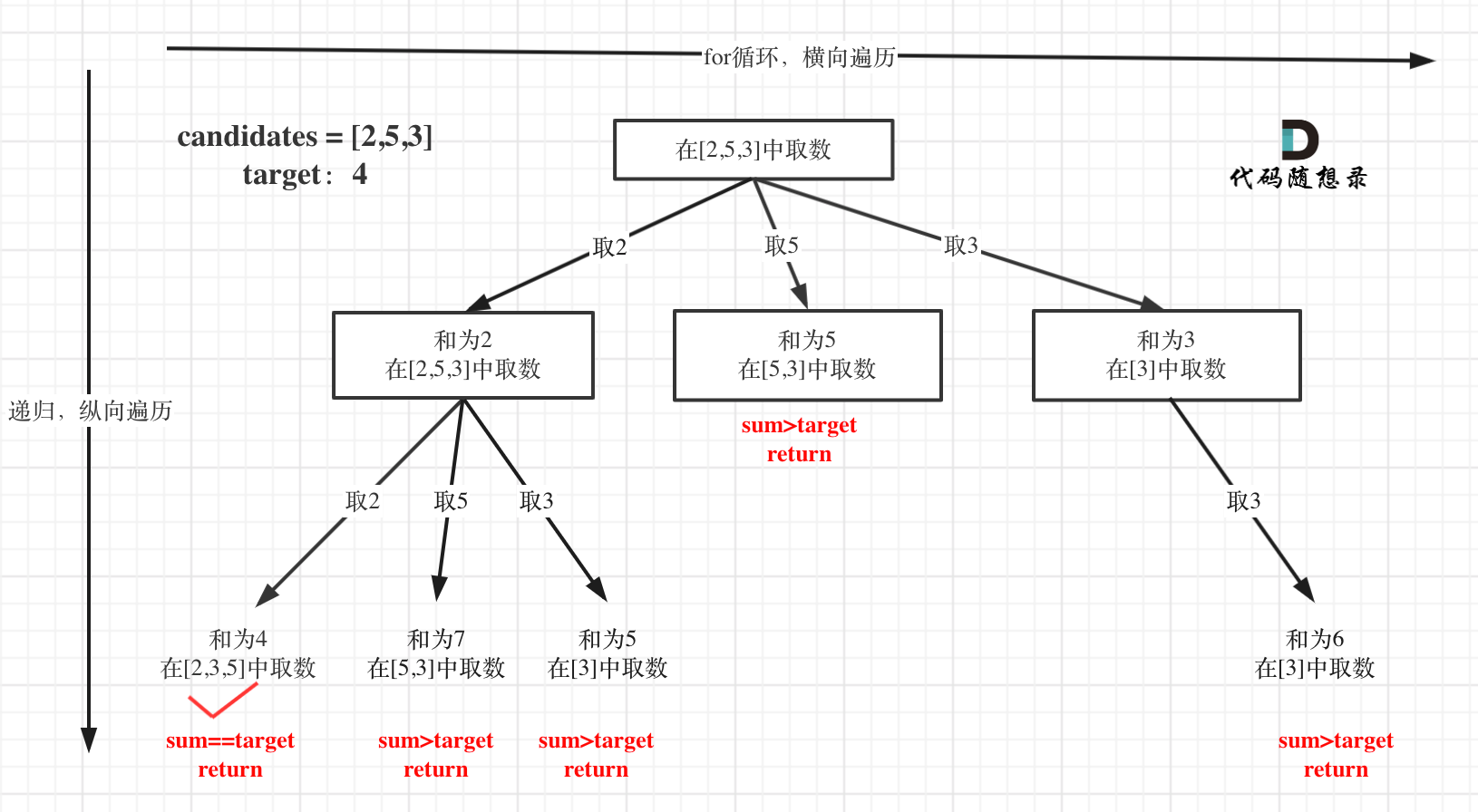
4. 组合总和 还是注意此时需要遍历的层数,比如第一层的元素为 arr[1] , arr[2] , arr[3] ...,那么下一层的元素就是 arr[1] , arr[2] , arr[3] ...,所以需要利用一个标志来控制遍历到的层数,并且开始位置索引为index,那么下一层的开始索引也是index, 组合总和.cpp
5. 组合总和II 本题目的不同之处在与待取元素的集合中存在重复的元素,但是有要求最终返回的集合中没有重复元素,所以如果直接利用最简单的组合方法,就会导致组合中的元素重复,比如 [1,7,1] target = 8 就会造成答案及集合中的元素重复,所以这里使用一个used数组来标记数据正在使用,如果一个数字正在使用,表示当前遍历到的数字和原来的数字在同样一个树枝上面,如果used的值为false,那么说明当前元素和待遍历元素在同一个树层上面需要跳过,同时注意去重: 组合总和II.cpp

组合问题的总结(三类组合问题):

• 最一般的情况: 数组中的元素不重复并且最终要求集合中的元素不重复,比如 1 2 3 解决方式: 直接利用一个索引startIndex用于控制当前遍历的层数,每一次递归直接传入curIndex + 1表示遍历后面的元素即可
• 数组中的元素不重复,但是数组中的每一个元素都可以使用多次,但是最终的集合中不可以出现相同的集合, 解决方法: 此时上面一个树层中的开始元素可以再一次和它自己组合,所以此时需要传递一个startIndex控制遍历索引,同时递归的时候传入curIndex本身作为下一层的开始的位置即可
• 数组中的元素重复,并且要求最终的组合中没有重复的组合,解决方法: 此时不可以重复使用元素,所以利用一个used来标记相同元素的位置,如果used[i] = false 表示当前遍历的相同元素和与它相同的元素在同一个树层,此时直接continue即可,如果used[i] = true,表示当前元素正在使用,所以此时和它相同的元素可以使用
• 另外注意给定元素个数的减枝操作和组合总和的减枝
• 各种情况的状态图如下:

1. 元素不重复并且组合不重复:
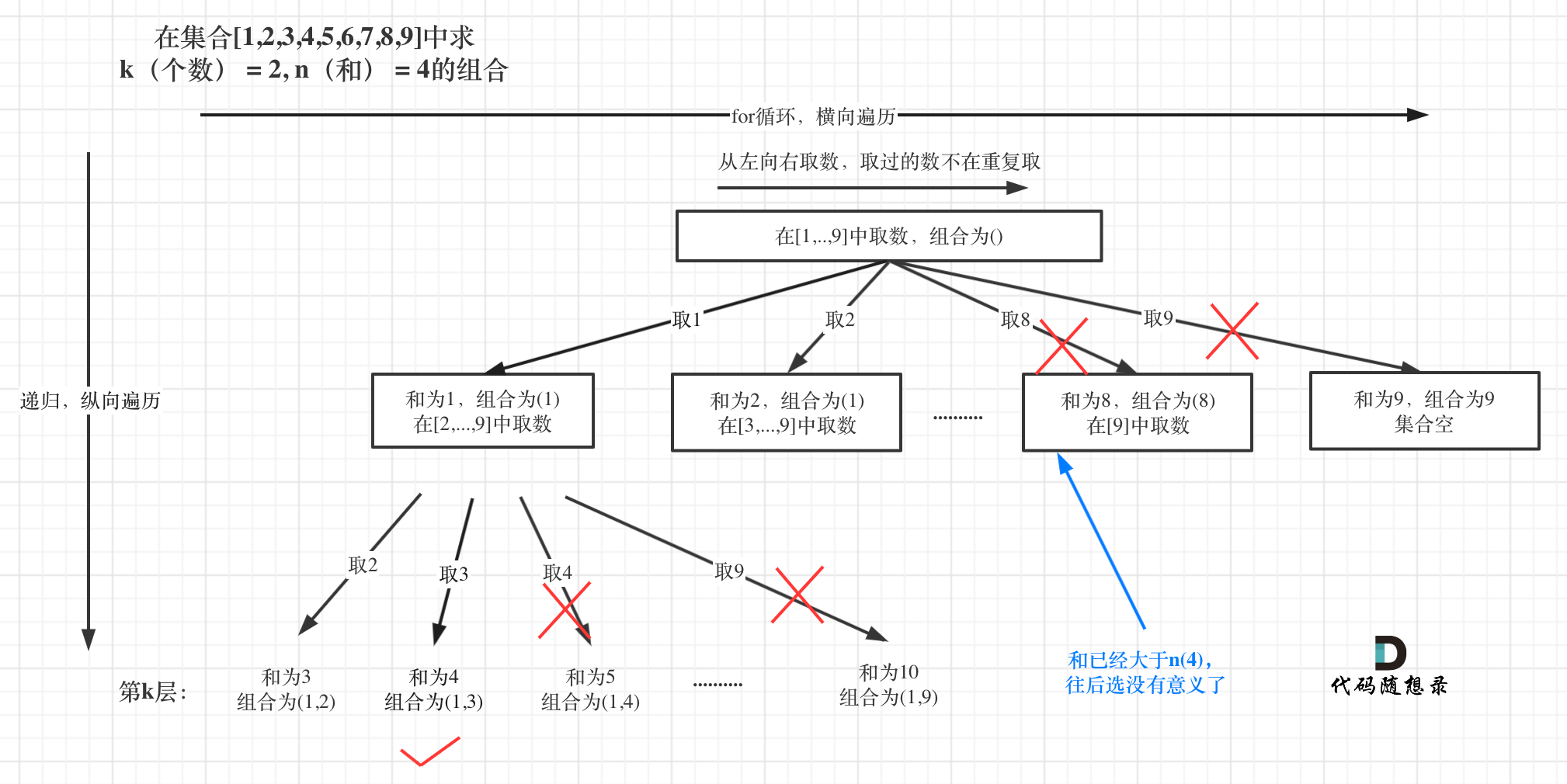
2. 元素不重复并且可以无限次使用要求组合不重复
3. 元素重复并且要求组合中的元素不重复(注意used数组的含义):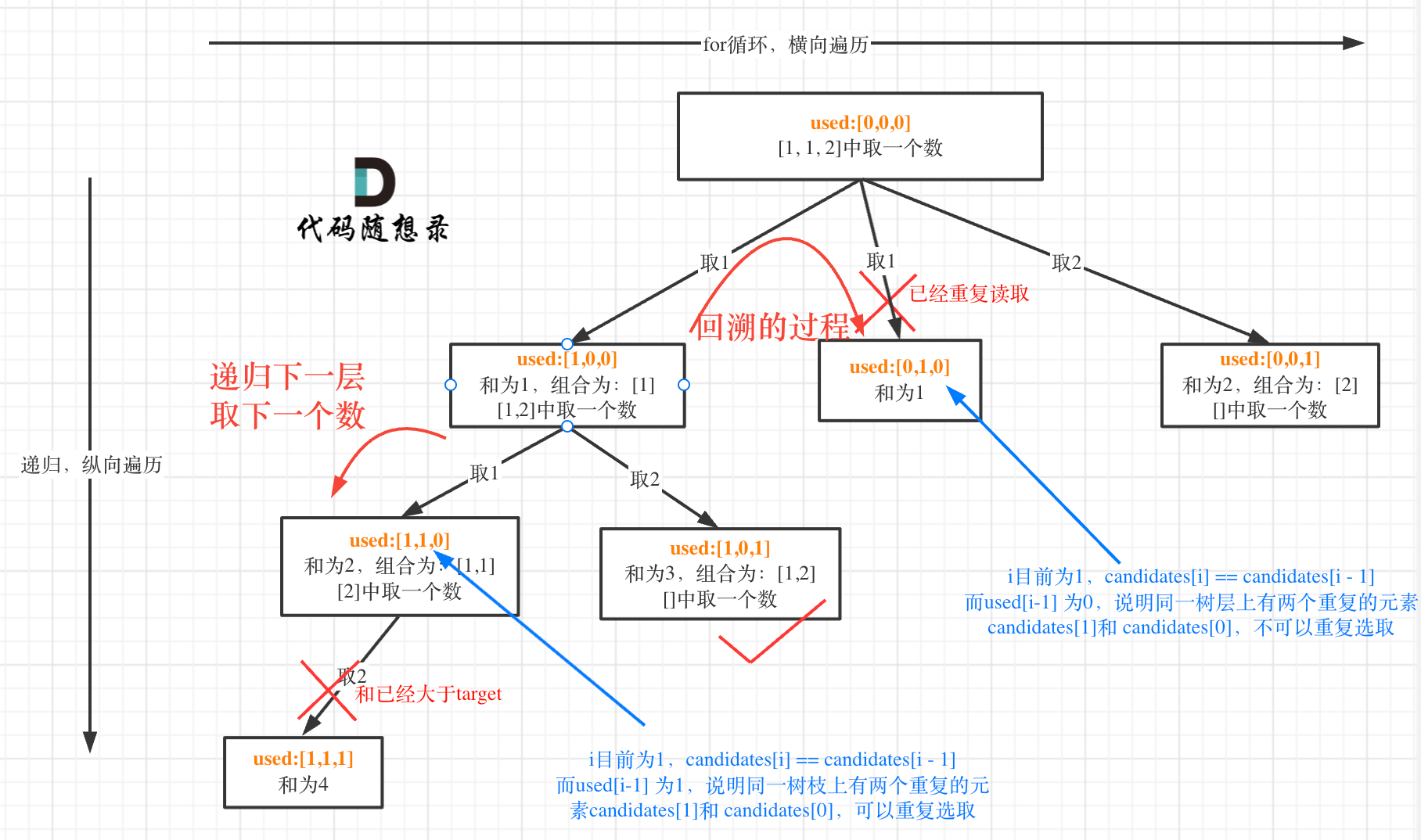

分割问题

1. 分割回文字符串 注意此时状态图的画法,和上面不同的是,这里需要使用分割线的位置来确定当前层数,至于减枝操作,就是如果遇到当前位置截取的字符串已经不是回文字符串了就可以直接返回了 分割回文字符串.cpp
2. 复原IP地址 这里就是分割字符串的操作的基础上面加上了对于子字符串的判断和最终分割的集合中的元素个数进行判断,这里还是需要一个变量来控制层数startIndex,这一个变量作为该层开始分割的起点,之后从这一个位置开始遍历知道集合的末尾,并且需要一个变量pointNum来标记字符串中.的个数,当个数为3的时候就可以判断剩余的部分是否满足要求即可 代码: 复原IP地址.cpp

• 对于分割问题,这里需要控制最开始的一个切点,在这一个切点开始,从后面的每一个字母后面进行切割操作从而达到回溯的效果,随着层数的底层,切痕的数量也会增加,startIndex表示上一个切痕后面的一个字母,移动后面的切痕即可截取一段字符串
• 分割回文字符串的树状图:
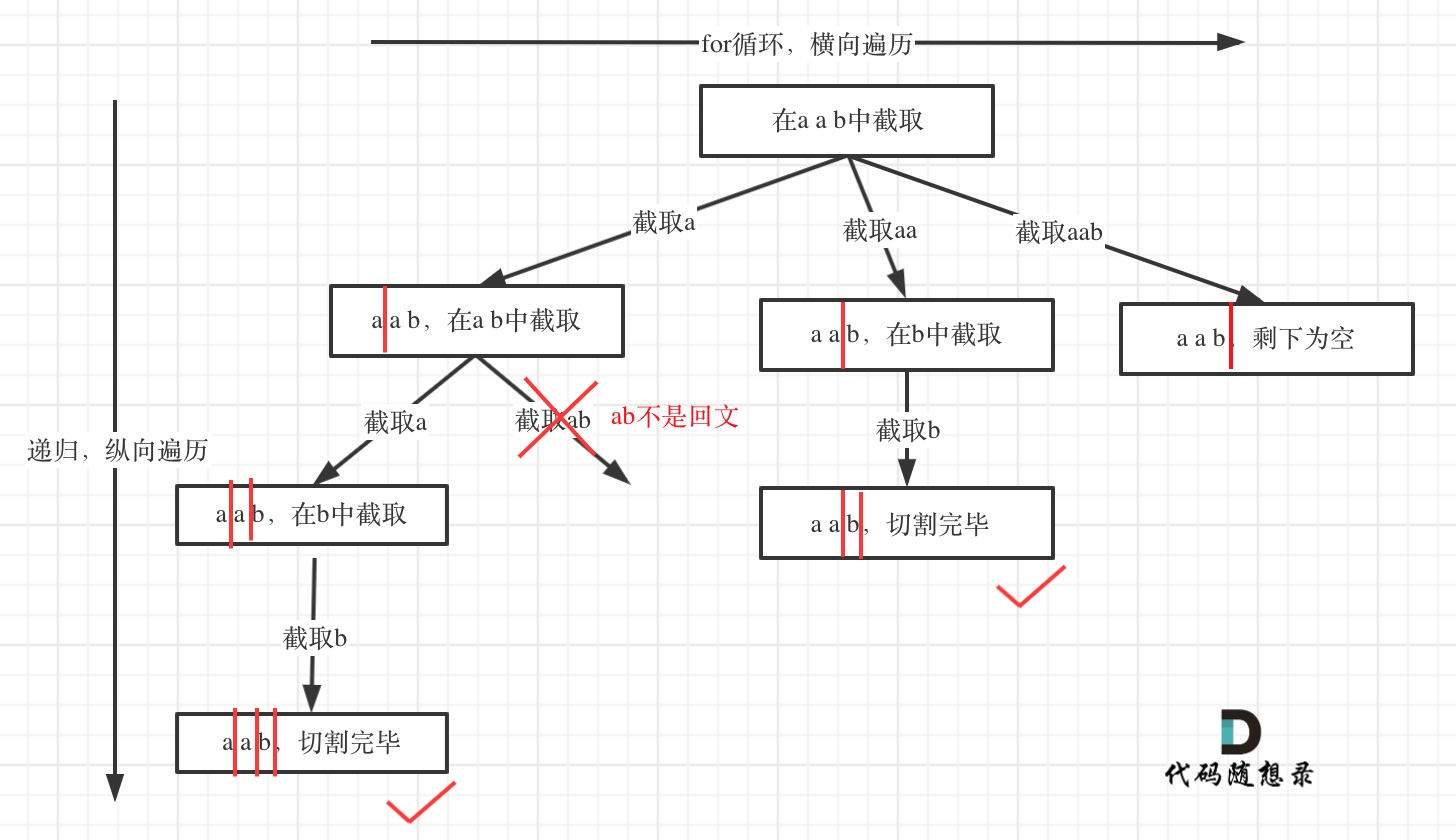
• 复原IP地址的树状图: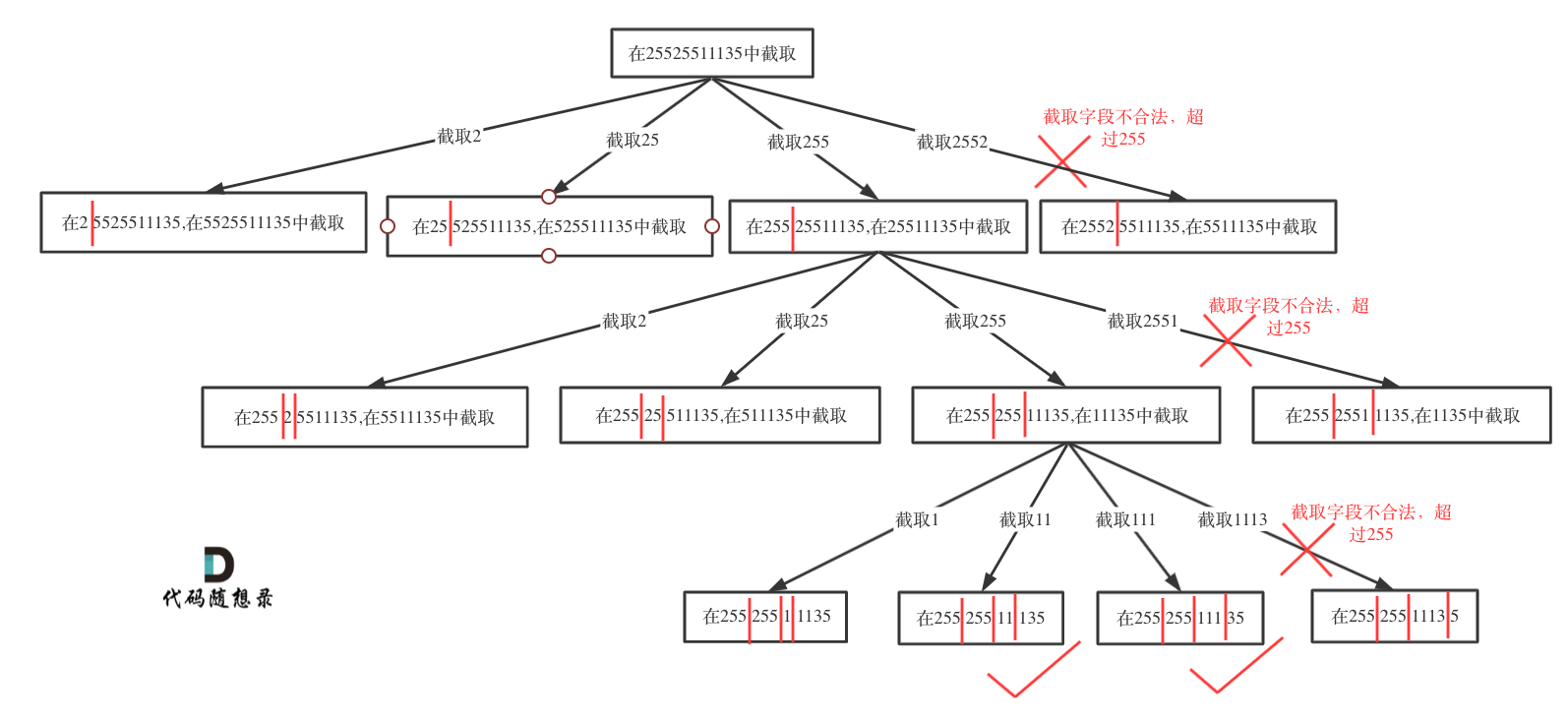

子集问题

1. 子集 注意回溯算法中for循环用于水平遍历,同时递归用于纵向遍历,所以如果需要收集所有的子集就需要收集树状图中的每一个节点,所以必须在回溯函数的入口处进行节点的收集,明确这一点之后子集问题就变成组合问题了(子集的一个特点就是不重复) 子集.cpp
2. 子集II 这里的特点就是数组中有重复元素但是最终的结果中没有重复元素(子集的性质),所以这里就可以转换为相应的组合问题 ,需要去重操作 子集II.cpp
3. 递增的子序列 这一个题目相对于前面的子集问题对于结果子集和进行限定了(递增并且长度大于2,所以这一次加入把子集加入到结果集中的时候需要判断长度),同时注意理解树状图,在选择下一层节点的时候上一层节点已经被加入到集合中了,所以只用选择大于这一个节点的下一个节点即可(此时也不需要使用used进行去除重复操作,这是由于每一层都需要去重操作,不是整体的去重复操作),所以可以每一层使用一个unordered_set进行去重复操作 递增的子序列.cpp

• 子集问题总结: 对于只是简单收集子集的问题,只需要收集每一层每一个节点位置的path即可,根据数组中元素的情况把子集问题转换为对应的组合问题即可,另外如果是需要收集满足条件的子集的情况,此时就需要进行条件判断之后才开始收集元素,同时需要画树状图来看如何去重
• 子集问题II树状图: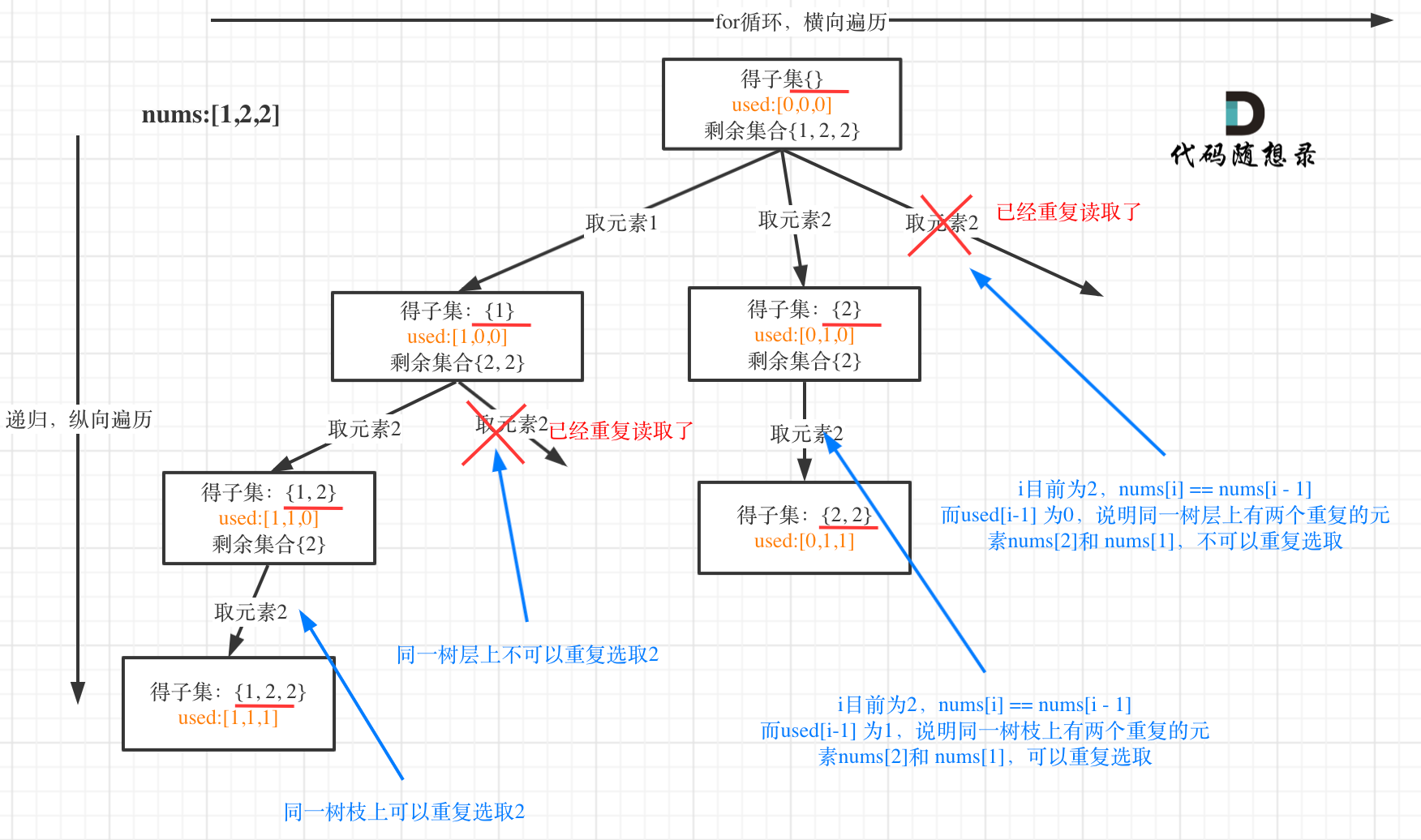
• 递增子序列树状图:

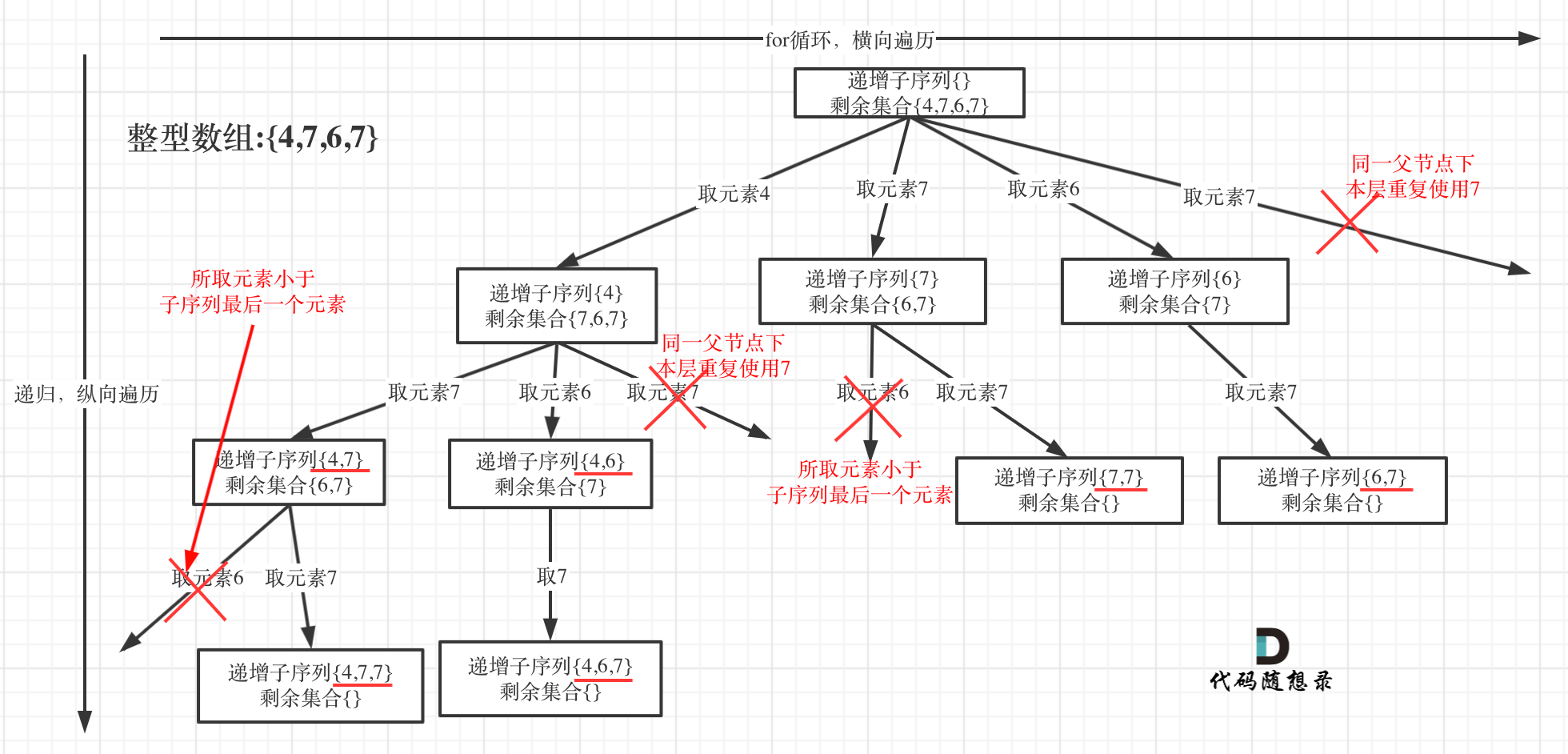
排列问题

1. 全排列 还是需要注意树状图的画法,单层递归逻辑中每一次选取的都是集合都是已经选取元素在原来集合中的补集,利用一个used数组记录元素是否被访问过,如果元素被访问过就跳过访问,另外此时由于不需要排除元素,所以不需要一个下标来控制索引 全排列.cpp
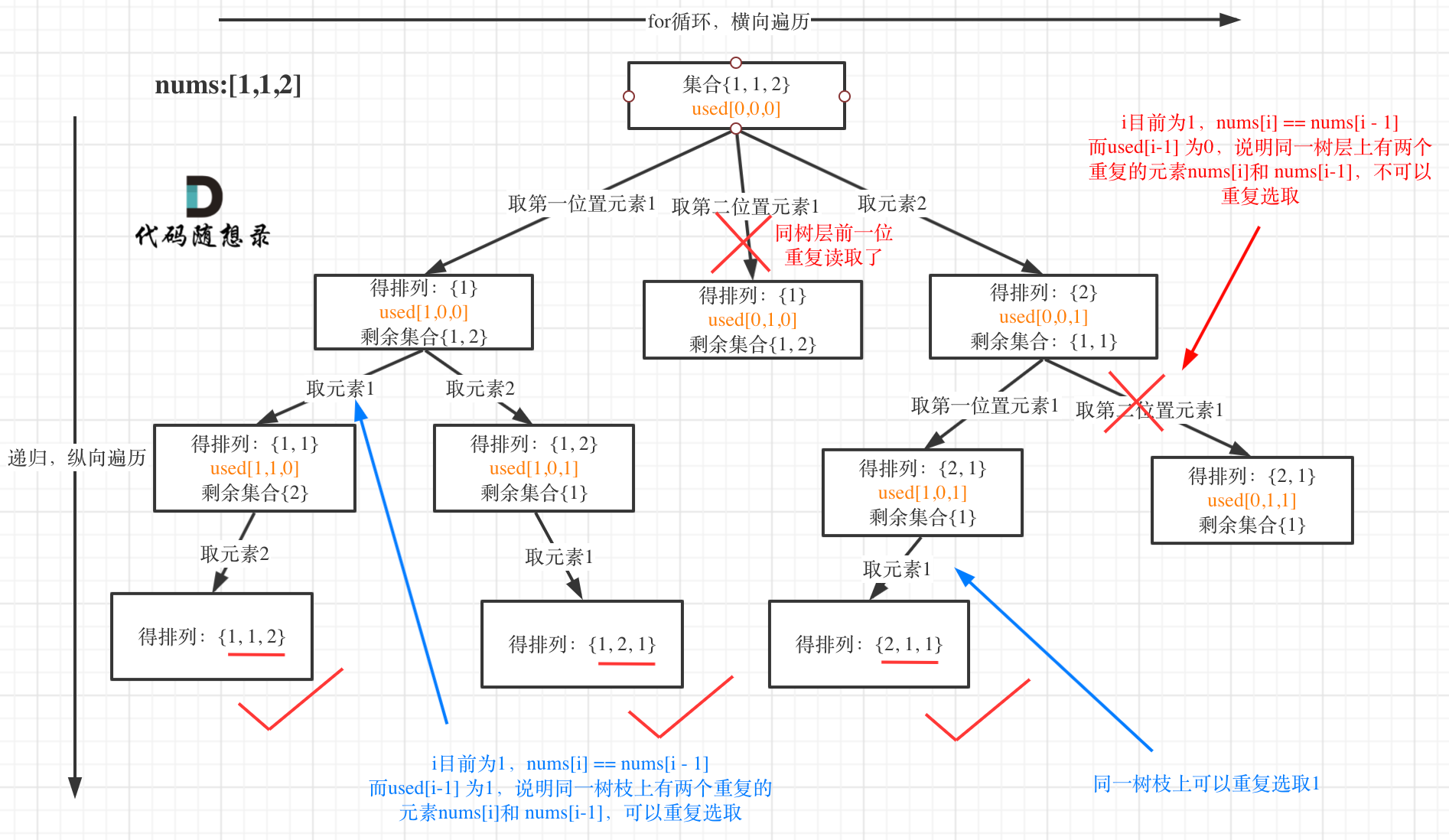
2. 全排列II 首先还是需要对于已经存在于集合中的元素进行去重复,同时对于一个集合中有重复元素但是要求在最终得到的排列中不可以有重复排列就需要使用used数组进行去重复,也就是只有元素出现在一个树枝中才可以使用,出现在一个树层中不可以使用,这两个过程中可以使用同样一个used数组(注意对于数组首先进行排序操作) 全排列II.cpp 去重方法还是同一个树层中去除重复元素,当然可以利用set集合进行去重操作

• 总结: 排列问题和子集问题以及组合问题的不同之处就在与需要获取集合中的所有元素,所以此时遍历层数不需要一个索引startIndex控制,而是需要一个数组used来找到没有访问过的节点(排除子集),其他的细节基本和组合总结的三种类型一致(没有重复,没有重复无限使用,有重复),总结三种问题的差异:
  • 组合问题: 无序并且一般需要满足特定的条件才可以收集节点
  • 子集问题: 无序,如果题目没有说明对于子集的条件,在递归函数入口处收集节点即可
  • 排列问题: 有序,每一次回溯都需要遍历数组,不需要索引指示层数
• 全排列的树状图:
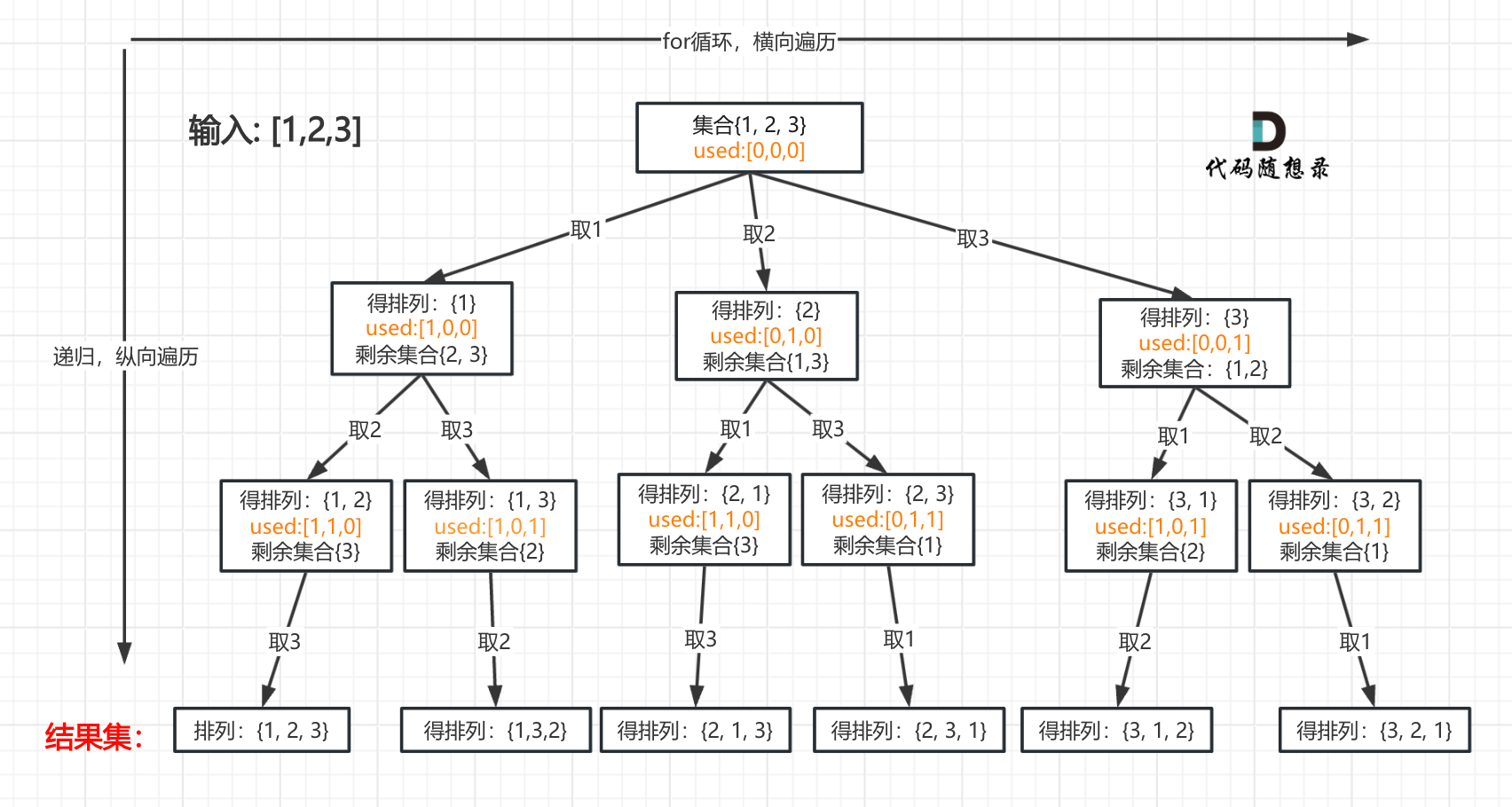
• 全排列II树状图(类似于组合II):

其他问题

• 其他问题包含八皇后和棋盘问题等

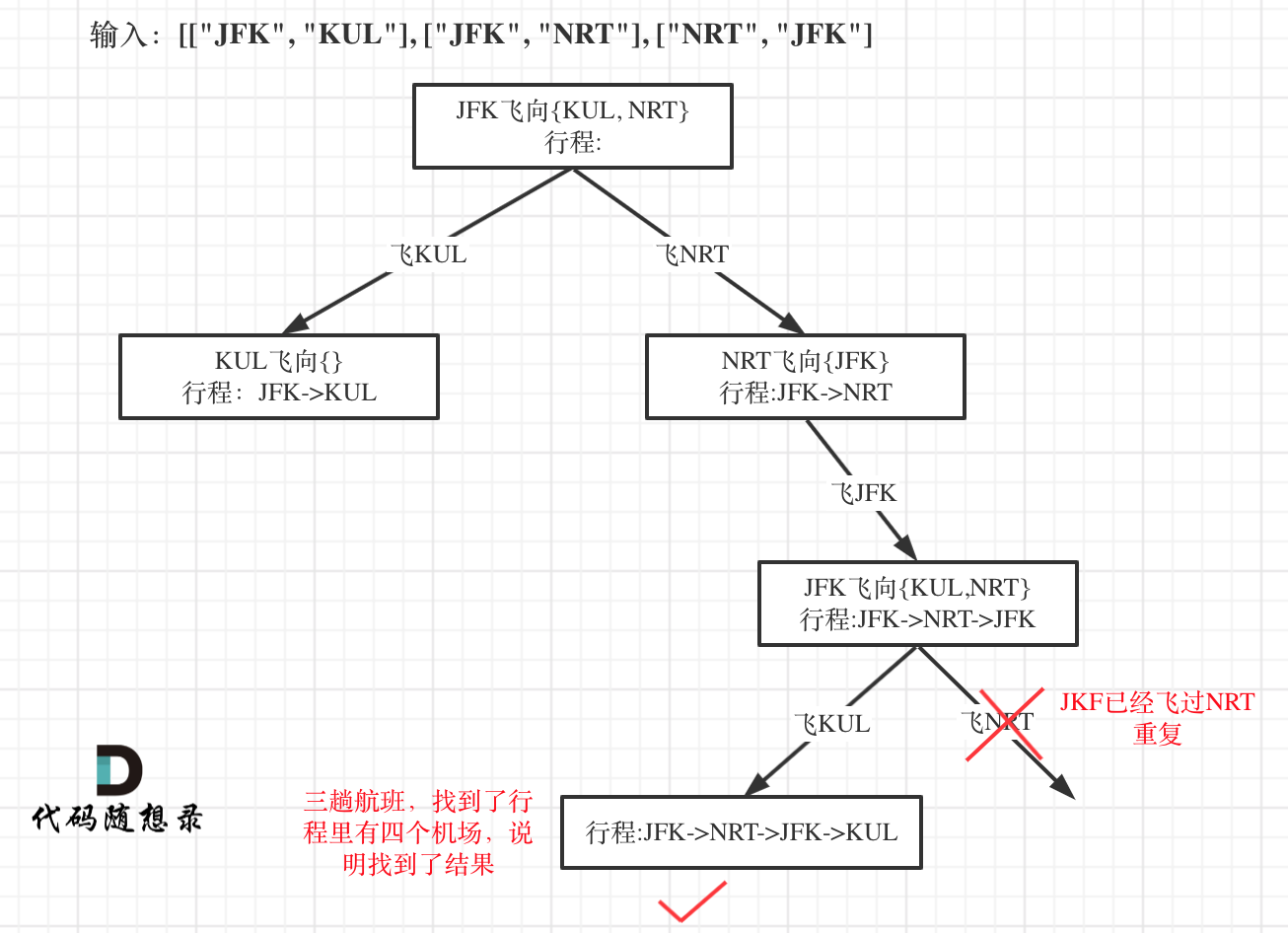
1. 重新安排行程 一道hard,本题的几个难点:
   1. 如何使用字典顺序来进行地点名称的排列(想到了使用哈希表,但是没有想到哈希表中的第二个元素可以使用map<string,int>类型对于key进行排序操作)
   2. 如果判断死循环(这里一一开始想的就是如果已经遍历了一条路径就可以直接在对应的map集合中移除路径了,但是原来使用的vector,所以回溯之后需要加回来就会比较困难,并且两个地点之间存储多张票的情况,所以这里使用map<string,int>叠二个值用于记录次数,每一次只用对于次数进行操作即可)
   3. 如果找到一条满足条件的路径之后立刻返回,这里回溯函数的参数使用bool类型表示是否找到满足条件的路径,找到就可以返回true 代码: 重新安排行程.cpp (实际上回溯就是深度优先遍历的一种体现,只不过需要利用深度优先遍历找到所有满足要求的节点)
2. N皇后 注意树状图的画法,也就是每一层的一个递归,需要传入每一层的参数来控制递归层数,想清楚之后很简单 N皇后.cpp
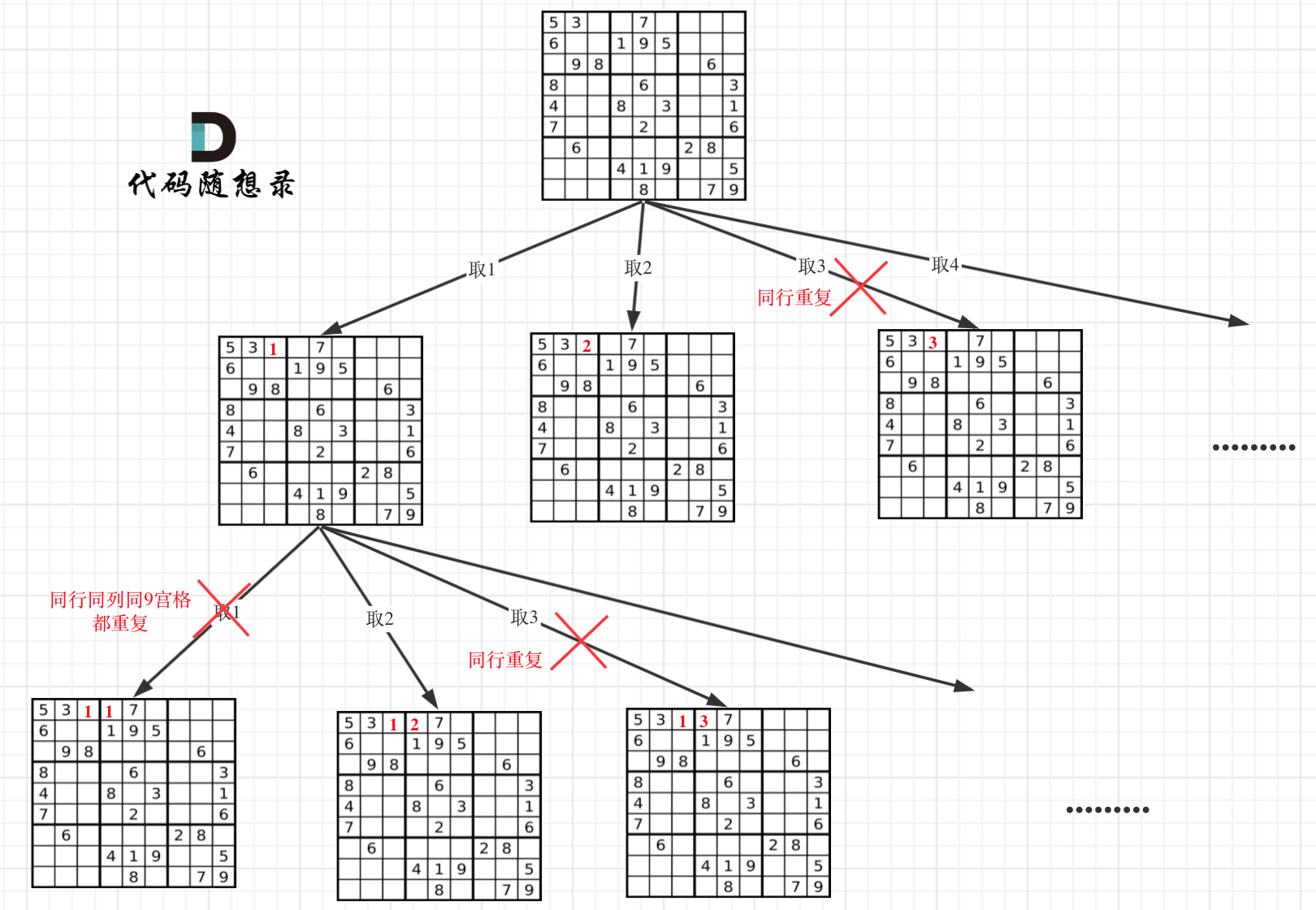
3. 求解数独 还是需要在脑子中构建出树状图,由于这里不用收集节点,只需要找到一个位置就可以返回了,所以回溯函数的返回值可以设置为bool类型,同时由于此时只是需要遍历棋盘找到空缺的位置所以在回溯函数也不需要传入一个参数来控制遍历的层数,最后就是如果对于任意一个节点此时无论填哪一个数字都无法使得数独满足要求就需要返回 false 求解数独.cpp

• 其他问题总结: 这一部分题目最重要的就是明确每一层回溯的对象,以及如何由上面一层来遍历下面一层(准确来说,下面一层就是上面一层的子集),最好的方式就是构建树状图,明确控制层数的变量以及递归函数的返回值得即可
• 重新安排行程的树状图如下:
• N皇后问题中的树状图: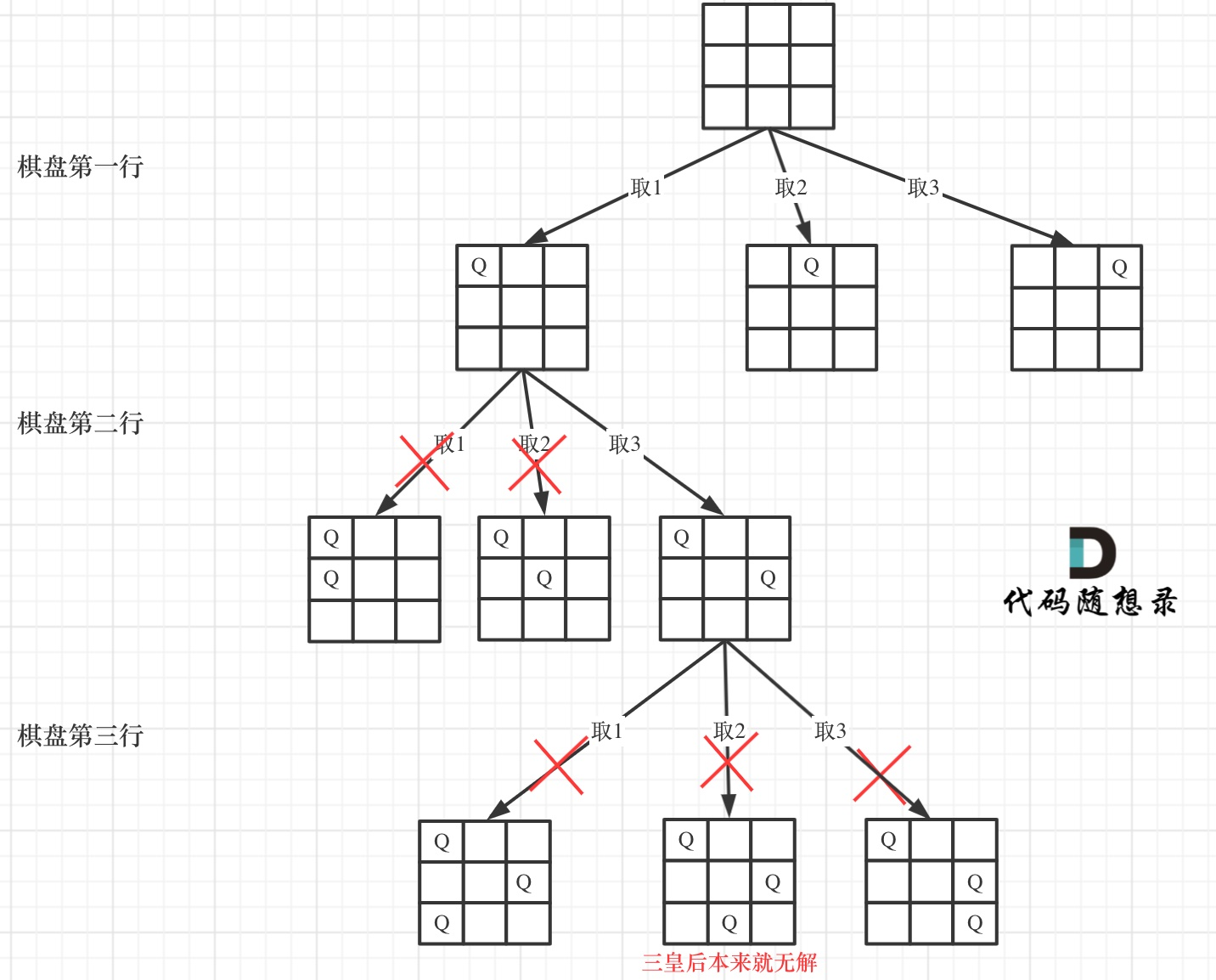
• 数独问题:

回溯算法总结

• 回溯算法可以解决的问题如下:
  • 组合问题
  • 分割问题
  • 子集问题
  • 排列问题
  • 棋盘问题
  • 深度优先遍历(深度优先遍历就是一种回溯算法)
• 总结解决方式:
  • 组合问题: 分三种情况,判断需要操作的数组中是否有元素重复以及集合中是否可以有重复元素以及元素是否可以使用多次(另外如果对于组合有条件限制注意减枝)
  • 分割问题: 此时需要回溯的变量就是分割线的位置,每一次回溯到一个分割线段之后,下一层的位置就是[startIndex,i] 其中i 就是一个循环变量,范围为startIndex -> (size-1)
  • 子集问题: 类似于组合问题,也就是在回溯函数入口的位置收割函数,如果有特定的条件还需要满足特定的条件,另外注意如果需要明确对于结果进行去重操作和对于每一层进行去重复操作的区别(其实可以混用)(也就是used数组和unordered_set其实是等效的)
  • 排列问题: 注意利用used数组进行去重复操作(本身结果不允许重复),注意此时used数组的作用:已经使用过的元素不可以再一次使用了,此时不需要一个变量来控制循环,另外这一个used数组也可以用于对于结果进行去重复,可以参考之前的排列问题
  • 棋盘问题: 明确树状图的画法和递归函数的写法即可
  • 深度优先遍历: 回溯函数的返回值为bool类型,注意什么时候可以找到正确的位置即可