cle动态规划解题步骤:
- 确定创建的
dp数组中对应下标元素的含义 - 确定递推公式
- 利用递推公式画出状态图,利用状态图确定数组的初始化
- 确定遍历的方式,比如背包问题中首先遍历背包还是首先遍历物品
动态规划例题
- 斐波那契数 简单的
dp斐波那契数.cpp - 爬楼梯 注意初始化 爬楼梯.cpp
- 使用最小花费爬楼梯 递推公式:
dp[i] = min(dp[i - 1] + cost[i - 1] , dp[i - 2] + cost[i - 2])使用最小花费爬楼梯.cpp - 不同路径 最基本二维
dp,递推公式:dp[i][j] = dp[i - 1][j] + dp[i][j - 1]遍历顺序:顺序遍历即可 不同路径.cpp - 不同路径II 此时递推公式还是上面的,但是此时如果周围的位置存在障碍,那么障碍的位置需要初始化为
0不同路径II.cpp - 拆分整数 这一个题目的递推公式并不是取决于周围的值,而是取决于前面的一切值得,比如对于
n,如果拆分成两个整数就是(i - k) * i, 如果拆分为多个整数那么就是dp[i - k] * k, 这里的k就是假设除去一个k之外看最大的乘积,注意这里的循环索引最大可以到i / 2这是由于均值不等式,所以尽可能平均分配才可以使得乘积最大,所以这一个数字不可能超过i / 2拆分整数.cpp - 不同的二叉搜索树 注意此时的递归函数又是比较难想,此时需要把不同的节点作为头节点,确定左右子树中节点的个数,从而确定总共的方案数量,比如对于
n个节点的树木,当使用j作为头接电脑的时候,左子树中的索引范围为1 - j - 1, 右子树的范围为j + 1 - n所以此时需要加上dp[j - 1] * dp[n - j]不同的二叉搜索树.cpp 01背包系列(背包的容量有限并且每一个物品只有两种状态: 取或者不取):- 01背包二维数组 注意这一个问题很重要,这里
dp[i][j]的含义就是在索引为范围为[0,i]内的元素中任意选取元素并且背包容量为j此时可以获得的最大价值 , 递推公式: 当背包容量无法容纳weight[i]的时候就延续之前的dp[i - 1][j]如果可以容纳weight[i]那么就选取是否装下第i个元素中最大的一个值,也就是:dp[i][j] = max(dp[i - 1][j] , dp[i - 1][j - weight[i]] + value[i])01背包二维数组.cpp - 01背包滚动数组 观察上面的递推公式,发现只是利用
i来控制索引,所以可以把二维数组压缩为一维数组,dp[j]表示背包容量为j的时候可以容纳的最大价值,初始化只需要把所有位置初始化为0即可,只是由于第一次遍历的时候不需要之前的状态(也就是没有物品的时候价值一定是0) ,另外在遍历的过程中,注意外层循环遍历物品,表示控制层数,内层循环遍历背包表示控制背包容量,需要从后面向前面遍历,这是由于遍历的过程中需要使用前面的数据这这里是为了放置覆盖前面的数据,递推公式:dp[j] = max(dp[j] , dp[j - weight[i]] + value[i])01背包滚动数组.cpp
- 01背包二维数组 注意这一个问题很重要,这里
- 分割等和子集 典型的
01背包问题,首先把背包容量设置为sum / 2,之后判断背包所有元素的和是否等于背包容量即可,这里注意weight和value是一致的,都是表示数值大小,递推公式:dp[j] = max(dp[j] , dp[j - nums[i]) + nums[i])分割等和子集.cpp - 最后一块石头的重量II 简单思考一下,粉碎之前两块是否的重量为
y + x,粉碎之后两块石头的重量为y - x, 此时重量的差值为2*x,所以此时只需要令背包的容量为sum / 2, 求出背包的最大可以容纳的石头重量即可,最后答案就是sum - 2*dp[sum / 2],递推公式同上: 最后一块石头的重量II.cpp
01背包总结,01背包的基本问题: 有m中物品,每一种物品的重量为weight[i],价值为value[i], 背包容量为n, 求解背包中可以装下的物品的最大值,这里的一个基本思路就是对于第i个物品分为两种情况讨论(也就是是否需要装这一个物品),从而就可以确定递推公式了,两种表现形式如下:- 二维数组:
dp[i][j]表示任意选取索引范围为[0,i]的物品装入到背包容量为j的背包可以获得的最大价值,遍历方式: 顺序遍历即可(注意此时如果无法装载第i样物品就直接继承之前即可) - 滚动数组:
dp[j]表示背包为j的物品在第i层可以装载物品的最大价值,遍历方式: 首先遍历物品,之后遍历容量并且需要倒序遍历容量(为了放置覆盖上一层在本层中需要使用的值)
- 二维数组:
01背包的用途除了处理传统的背包问题,还可以用于处理给定一个最大值,求解通过装载一定元素到达距离这一个最大值最近点的值
- 目标和 类似于上面的题目,也就是对于求和的题目都应该想到背包问题(背包问题的重点就在于是否放入第
i中物品),但是主要这里的递推公式:dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]]注意在列初始化的时候如何找到和为0的情况,也就是确定和为0的总共情况数量 - 一和零 注意
01背包的思想就在与是否去除第i个元素,滚动数组和多维数组的方法都是一样的,这里就是多维情况下的01背包问题 , 注意使用三位数组的初始化方式: 一和零.cpp
- 背包问题的种类:
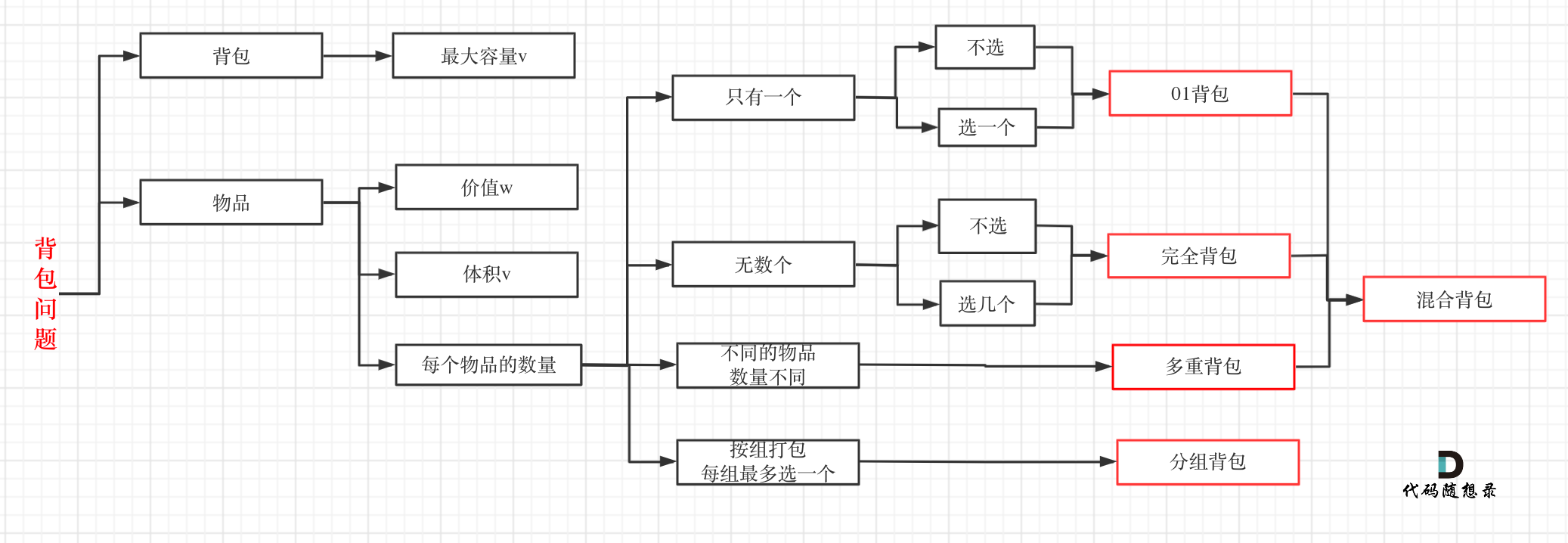
- 完全背包问题: 和
01背包问题不同的地方就在于完全背包问题中元素可以去取出无数次,所以相对于01背包问题利用滚动数组的时候,遍历第二层的时候就需要注意,此时应该正序遍历,就是为了后面可以用到前面的结果,比如也就是遍历到(i,j)的时候就是需要把i装入到背包中,从后面向前面遍历,前面的没有改变(也就是没有装下i) ,但是从前面向后面遍历,前面的元素已经装下i了,后面的元素可以重复装 ,只是遍历顺序不同 完全背包.cpp
- 零钱兑换II 完全背包问题,还是分为第
i个物品是否装入到背包中,递推公式:dp[j] += dp[j - coins[i]], 但是注意测试用例中有超过int的版本,所以需要使用比较大的无符号整型变量 , 所以需要使用uint64_t零钱兑换 1.cpp - 组合总和IV 注意对于完全背包问题:
- 如果需要求解组合数,那么就需要外层遍历物品,内层遍历背包容量
- 如果要求求解排列数,那么就需要外层遍历背包容量,内层遍历物品 组合总和IV.cpp
- 爬楼梯(进阶版) 两种思路: 爬楼梯(进阶版).cpp
- 抽象为背包问题: 注意此时需要求解的是排列数,所以需要首先遍历容量之后遍历背包,递推公式为:
dp[i] += dp[i - j] - 不抽象为背包问题: 此时的递归公式为:
$$ dp[i] = \sum\limits_{k = i - m}^{i - 1} dp[k] $$
- 抽象为背包问题: 注意此时需要求解的是排列数,所以需要首先遍历容量之后遍历背包,递推公式为:
- 零钱兑换 递推公式:
dp[j] = min(dp[j] , dp[j - coins[i]] + 1)注意此时需要注意初始化方式:dp[0] = 0 , dp[j] = INT_MAX,当元素为INT_MAX的时候就表示没有初始化,没有满足要求的组合 零钱兑换 1.cpp - 完全平方数 和上面的题目一个样,只不过这里的目标数组可以看成:
dp[i] = i*i完全平方数字.cpp - 单词拆分 比较难想,注意此时只需要考虑
s,只需要把s划分为不懂得段并且在字典中寻找对应的元素即可 ,dp[j]表示长度为j的从头开始的子字符串是否可以由字典中的元素组成,递推公式:if(us.find(s.substr(j , i - j)) != us.end() && dp[j]) dp[i] = true注意此时由于需要求解排列数,所以需要首先遍历背包(也就是dp),之后遍历元素,也就是i之前的元素 (元素是子串,背包是字符串) 单词拆分.cpp - 多重背包问题 特征就是一个物品可以使用有限次数,解决方法就是把可以使用有限次数的物品拆分为可以使用次数个物品数量,从而转换为
01背包问题,注意01背包问题中是顺序遍历物品的,所以只需要每一次在内层循环中遍历多次物品(也就是在有限次数下遍历物品)即可 多重背包.cpp
- 背包问题总结:
- 背包问题的特点如下:
01背包: 每一物品只可以使用一次- 完全背包: 每一个物品可以使用多次
- 多重背包: 每一物品可以使用有限次
- 背包问题解决方法:
01背包利用二维数组或者滚动数组,注意利用滚动数组的时候需要内层反序遍历背包容量,外层遍历物品- 完全背包利用滚动数组,但是注意遍历背包和遍历物品的顺序,并且遍历背包容量的过程总是从左到右的(比如从
weight[i]到s.size()) ,注意遍历顺序:- 如果是组合数,外层遍历物品,内层遍历背包
- 如果是排列数,外层遍历背包,内层遍历物品(注意条件判断)
- 多重背包问题: 把物品的使用此时看成新的各种物品从而把问题转换为
01背包的问题即可
- 背包问题的特点如下:
- 注意背包问题的精髓在与递推公式:
dp[j] = max(dp[j] , dp[j - weight[i]] + value[i])递推公式表明的是第i件物品时候选取
- 打家劫舍 还是类似于背包问题,就在于是否需要取出第
i个元素,递推公式:dp[i] = max(dp[i - 1] , dp[i - 2] + nums[i]),需要初始化前面两个元素 打家劫舍.cpp - 打家劫舍II 考虑两种情况: 偷第一家,不偷第一家两种情况,可以利用一个数组
dp[i][2]表示相应的情况,dp[i][0]表示不偷第一家的情况,dp[i][1]表示偷第一家的情况,注意初始化方式即可 打家劫舍II.cpp - 打家劫舍III 每一个根节点有两种情况,偷或者没有被偷,所以需要分别讨论这两种情况,所以可以使用一个
vector<int>数字表示这两种情况:dp[1]表示节点被偷,dp[0]表示节点没有被偷走 打家劫舍III.cpp - 买卖股票的最佳时机(特点: 只允许一次买卖) :
- 第一种思路: 在遍历的过程中不断找到前面元素的最小值和后面的元素与最小值的最大差值即可
- 第二种思路: 利用动态规划思想,每一个节点由两种状态,
dp[i][0]为第i天不持有股票的最大利润,dp[i][1]为第i天持有股票的最大利润,递推公式如下:dp[i][0] = max(dp[i - 1][0] , dp[i - 1][1] + prices[i])和dp[i][1] = max(dp[i - 1][1] , -prices[i])买卖股票的最佳时机.cpp
- 买卖股票的最佳时机II (特点: 允许多次买卖)
- 动态规划:
dp[i][j]的含义和上面一样,递推公式:dp[i][0] = max(dp[i - 1][0] , dp[i - 1][1] + prices[i])dp[i][1] = max(dp[i - 1][1] , dp[i - 1][0] - prices[i]) - 贪心算法: 每一次只要后面的价格大于前面的价格就可以叠加了 买卖股票的最佳时机II.cpp
- 动态规划:
- 买卖股票的最佳时机III (特点: 可以买卖有限次数) 定义不同的状态:
0表示不操作 ,1表示第一次买入之后,2表示第一次卖出之后,3表示第二次买入之后,3表示第二次卖出之后 ,之后通过递推公式即可求解 买卖股票的最佳时机III.cpp - 买卖股票的最佳时机IV (特点: 规定了买卖次数),需要定义
2*k + 1中状态,注意递推公式 买卖股票的最佳时机IV.cpp - 买卖股票的最佳时机含冷冻期 这一个题目最难的就是规划状态,注意如何进行状态的规划,首先一定需要清除各种状态之间的转换关系,比如今天卖出就会导致下一天处于冷冻期,所以大体上可以分为持有股票与否,细分又可以范围今天是否卖出股票,是否处于冷冻期等 买卖股票的最佳时机含有冷冻期.cpp
- 买卖股票的最佳时机含手续费 还是两种状态,注意递推公式即可,注意在卖出的时候加上手续费 买卖股票的最佳时机含手续费.cpp
- 股票问题总结: 股票问题引出了动态规划的一种新的题型,也就是同一个节点具有不同的状态,需要利用一个多为数字来记录不同节点的不同状态从而确定相应的递推公式,特别需要注意状态的划分,在状态机中需要具有连续性:
- 买卖股票问题 --> 只可以买卖一次
- 买卖股票问题II --> 可以买卖无数次
- 买卖股票问题 III --> 可以买卖
2次 - 买卖股票问题 IV --> 可以买卖
k次 - 含冷冻期 --> 注意状态机的应用
- 含手续费 --> 注意递推公式的使用即可
- 最长递增自序列 又是一个新的开端,这里的
dp[i]不仅仅与前面的状态有关,同时也和之前的状态有关,注意dp[i]表示以索引为i的数字结尾的最长自序列 最长递增子序列.cpp - 最长连续递增子序列 还是只和前面的状态有关,可以利用动态规划或者贪心 最长连续递增子序列.cpp
- 最长重复子数组 注意这里需要求解的子数组需要是连续的,并且注意定义的时候可以定义:
dp[i][j]表示长度为i的num1子串和长度为1的nums2子串的公共子串的长度,所以递推公式:if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1, 另外也可以使用一维数组模拟(但是注意和一维dp,01背包问题中一样,需要内层反序遍历): 最长重复子数组.cpp (前面的元素只是计算一次 -> 反序,需要多次使用 -> 正序) 此时注意前面的元素不可以重复利用(比如num1[i - 1] != nums2[j - 1]) 的时候需要清空而不是把前面的加上 - 最长公共子序列 注意这里的子序列可以是不连续的,有一点编辑距离问题的意思,这里还是使用
dp[i][j]表示长度为i,j的字符串的最长公共子串,注意dp[i][j]的状态由dp[i - 1][j - 1]和dp[i - 1][j] 和 dp[i][j - 1]决定, 最长公共子序列.cpp - 不相交的线 和上面一样 不相交的线.cpp
- 最大子数组和 动态规划的思路比较好想,类似于前面的递增子序列问题,只需要考虑
j结尾即可,递推公式:dp[j] = dp[j - 1] < 0 ? nums[j] : dp[j - 1] + nums[j], 也可以使用贪心算法: 最大子数组和 1.cpp - 判断子序列 这里还是一样,对于这里的序列的题目(也就是编辑距离的题目),总是考虑新加入到序列中的两个元素的关系(比如这里就是
dp[i]和鄂dp[j]) , 这里的递推公式:if(s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] else dp[i][j] = dp[i][j - 1]判断子序列.cpp - 不同的子序列 还是和其他的编辑距离的题目一样,只需要关注后面两个元素的比较即可:
if(s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1] else dp[i][j] = dp[i - 1][j]注意此时结果会发生溢出,所以可以使用uint64_t或者unsigned long long不同的子序列.cpp - 两个字符串的删除操作 还是比较常规的编辑距离的问题,这里还是考虑最后一个字母,相等的时候删除前面的字母即可,不相等的时候分为三种情况讨论即可(删除第一个,删除第二个,删除所有) 两个字符串的删除操作.cpp
- 编辑距离 还是典型的编辑距离的问题,还是哪一个方法,
dp[i][j]分别表示长度为i和j的满足要求的子串进行变化需要的次数 , 还是分为两种情况(也就是新加入的两个字母是否想等): 相等就不需要修改了,如果不相等可以分为删除一个,添加一个或者改变一个的策略,根据策略的不同就可以得到递推公式了:dp[i][j] = min(dp[i - 1][j] , dp[i][j - 1] , dp[i - 1][j - 1]) + 1编辑距离.cpp
- 编辑距离总结: 编辑距离问题的通用方法就是,首先可以定义
dp[i][j]为长度分别为i和j的子串或者子数组需要进行题目中给定的变化的最小次数,之后需要分别讨论word1[i - 1] == word2[j - 1]和word1[i - 1] != word2[j - 1]的情况,第二种情况中有需要分别讨论增删改查的最小次数
- 回文子串 经典题目,首先判断回文子串,之后统计回文子串的个数即可,注意
dp[i][j]表示索引范围为[i,j]内的字符串是否为回文子串,这里可以通过判断s[i]和s[j]和之间的字符串确定,递推公式:dp[i][j] = dp[i + 1][j - 1]所以注意遍历顺序从下到上,从左边到右,同时注意此时遍历包含边界所以不需要初始化,另外一种方法就是中心扩散法,测试可以考虑字符串的长度是奇数还是偶数,可以以中间一个为中心或者两个为中心 回文子串.cpp - 最长的回文子串长度 和上面一个题目一个样子,都是需要考虑前后两个方面,此时相等的是的递推公式为:
dp[i][j] = dp[i + 1][j - 1] + 2不相等的时候的递推公式为:dp[i][j] = max(dp[i][j - 1],dp[i + 1][j],注意画出状态图从而确定递推公式的推导方向: 最长的回文子串长度.cpp